
 如圖所示,在直角坐標(biāo)系中畫出將“小船”先向下平移2個單位,再向右平移3 個單位的圖形,并計算出小船的面積.
如圖所示,在直角坐標(biāo)系中畫出將“小船”先向下平移2個單位,再向右平移3 個單位的圖形,并計算出小船的面積.
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
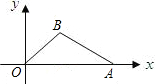 sin∠BOA=
sin∠BOA=| 3 | 5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
| m | x |
 1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連接AD、DC、CB.
1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連接AD、DC、CB.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
如圖所示,在直角坐標(biāo)平面內(nèi),函數(shù)的圖象經(jīng)過A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連結(jié)AD、DC、CB.
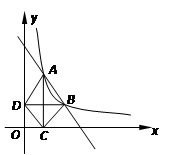
1.若△ABD的面積為4,求點B的坐標(biāo)
2.求證:DC∥AB
3.四邊形ABCD能否為菱形?如果能,請求出四邊形ABCD 為菱形時,直線AB的函數(shù)解析式;如果不能,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:

查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2012年江蘇省鹽城市大豐市中考數(shù)學(xué)一模試卷(解析版) 題型:解答題
 的圖象經(jīng)過A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連接AD、DC、CB.
的圖象經(jīng)過A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,連接AD、DC、CB.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com