
 ,
, AP=1,
AP=1,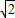 PD=
PD= .
.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:


查看答案和解析>>
科目:初中數學 來源:2012屆江蘇省興化市楚水初級中學九年級中考模擬數學試卷(帶解析) 題型:解答題
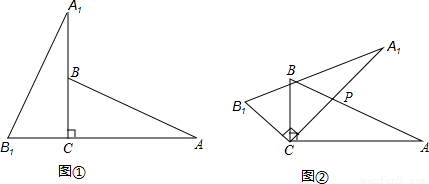
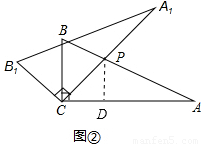
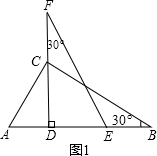
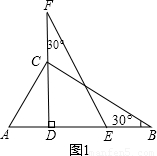
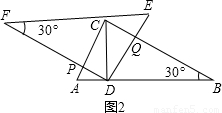
如圖(1),我們將相同的兩塊含30°角的直角三角尺Rt△DEF與Rt△ABC疊合,使DE在AB上,DF過點C,已知AC=DE=6。將圖(1)中的△DEF繞點D逆時針旋轉(DF與AB不重合),使邊DF、DE分別交AC、BC于點P、Q,如圖(2)。
(1)求證:△CQD∽△APD
(2)連結PQ,設AP=x,求面積S△PCQ關于x的函數關系式;
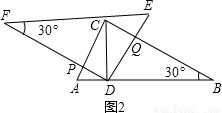
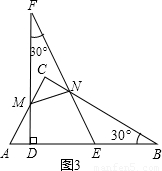
(3)將圖(1)中的△DEF 向左平移(A、D不重合),使邊FD、FE分別交AC、BC于點M、N,如圖(3),連結MN,試問△MCN面積是否存在最大值、如不存在,請說明理由;如存在請求出S△MCN 的最大值,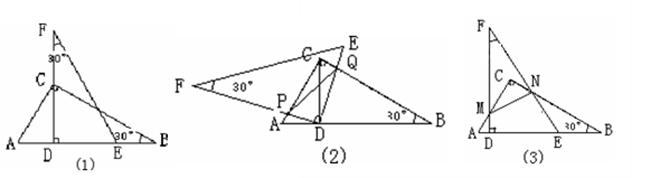
查看答案和解析>>
科目:初中數學 來源:2011-2012學年江蘇省興化市九年級中考模擬數學試卷(解析版) 題型:解答題
如圖(1),我們將相同的兩塊含30°角的直角三角尺Rt△DEF與Rt△ABC疊合,使DE在AB上,DF過點C,已知AC=DE=6。將圖(1)中的△DEF繞點D逆時針旋轉(DF與AB不重合),使邊DF、DE分別交AC、BC于點P、Q,如圖(2)。
(1)求證:△CQD∽△APD
(2)連結PQ,設AP=x,求面積S△PCQ 關于x的函數關系式;
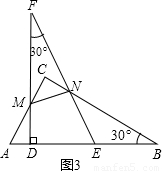
(3)將圖(1)中的△DEF 向左平移(A、D不重合),使邊FD、FE分別交AC、BC于點M、N,如圖(3),連結MN,試問△MCN面積是否存在最大值、如不存在,請說明理由;如存在請求出S△MCN 的最大值,

查看答案和解析>>
科目:初中數學 來源:第34章《二次函數》中考題集(47):34.4 二次函數的應用(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:第2章《二次函數》中考題集(47):2.8 二次函數的應用(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com