
【題目】推理填空.如圖,已知∠1=∠2,∠B=∠C,可推得AB∥CD,理由如下:
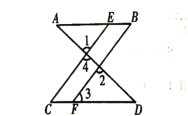
解:因為∠1=∠2(已知),且∠1=∠4( )
所以∠2=∠4(等量代換)
所以CE∥BF( )
所以∠ =∠3( )
又因為∠B=∠C(已知),所以∠3=∠B( )
所以AB∥CD ( )
 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ACB=90°,點M為BA延長線上一點,∠ABC的平分線BE和∠CAM的平分線AD相交于點P,分別交AC和BC的延長線于E,D.過P作PF⊥AD交AC的延長線于點H,交BC的延長線于點F,連接AF交DH于點G,則下列結論:①∠APB=45°;②PF=PA;③DG=AP+GH;④BD﹣AH=AB.其中正確的是_____(填序號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲船勻速順流而下從![]() 港到
港到![]() 港,同時乙船勻速逆流而上從
港,同時乙船勻速逆流而上從![]() 港到
港到![]() 港,
港,![]() 港處于
港處于![]() 、
、![]() 兩港的正中間,某個時刻,甲船接到通知需立即掉頭逆流而上到
兩港的正中間,某個時刻,甲船接到通知需立即掉頭逆流而上到![]() 處,到
處,到![]() 處后迅速按原順流速度駛向
處后迅速按原順流速度駛向![]() 港,最后甲、乙兩船都到達了各自的目的地.甲、乙兩船在靜水中的速度相同,設甲、乙兩船與
港,最后甲、乙兩船都到達了各自的目的地.甲、乙兩船在靜水中的速度相同,設甲、乙兩船與![]() 港的距離之和為
港的距離之和為![]() ,行駛時間為
,行駛時間為![]() ,
,![]() 與
與![]() 的部分關系如圖,則當兩船在
的部分關系如圖,則當兩船在![]() 、
、![]() 間某處相超時,兩船距離
間某處相超時,兩船距離![]() 港的距離為________千米.
港的距離為________千米.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
材料1:對于一個關于![]() 的二次三項式
的二次三項式![]() ,除了可以利用配方法求該多項式的取值范圍外,愛思考的小川同學還想到了其他的方法;比如先令
,除了可以利用配方法求該多項式的取值范圍外,愛思考的小川同學還想到了其他的方法;比如先令![]() ,然后移項可得:
,然后移項可得:![]() ,再利用一元二次方程根的判別式來確定
,再利用一元二次方程根的判別式來確定![]() 的取值范圍,請仔細閱讀下面的例子:
的取值范圍,請仔細閱讀下面的例子:
例:求![]() 的取值范圍;
的取值范圍;
解:令![]()
![]()
![]()
![]()
![]() ;
;
材料2:在學習完一元二次方程的解法后,愛思考的小川同學又想到仿造一元二次方程的解法來解決一元二次不等式的解集問題,他的具體做法如下:
若關于![]() 的一元二次方程
的一元二次方程![]() 有兩個不相等的實數根
有兩個不相等的實數根![]() 、
、![]() ,則關于
,則關于![]() 的一元二次不等式
的一元二次不等式![]() 的解集為:
的解集為:![]() 或
或![]() ;則關于
;則關于![]() 的一元二次不等式的
的一元二次不等式的![]() 的解集為:
的解集為:![]() .
.
材料3:若關于![]() 的一元二次方程
的一元二次方程![]() 有兩個不相等的實數根
有兩個不相等的實數根![]() 、
、![]() ;則
;則![]() ;
;![]() ,我們稱之為韋達定理;
,我們稱之為韋達定理;
請根據上述材料,解答下列問題:
(1)若關于![]() 的二次三項式
的二次三項式![]() (
(![]() 為常數)的最小值為
為常數)的最小值為![]() ,則
,則![]() ________.
________.
(2)求出代數式![]() 的取值范圍.
的取值范圍.
(3)若關于![]() 的代數式
的代數式![]() (其中
(其中![]() 、
、![]() 為常數,且
為常數,且![]() )的最小值為
)的最小值為![]() ,最大值為4,請求出滿足條件的
,最大值為4,請求出滿足條件的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個長5m的梯子AB,斜靠在一豎直的墻AO上,這時AO的距離為4m,如果梯子的頂端A沿墻下滑1m至C點.
(1)求梯子底端B外移距離BD的長度;
(2)猜想CE與BE的大小關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明去文具店買文具,他與售貨員的對話如下:
小明:你好.我要購買5支黑色水筆和3本筆記本.
售貨員:好的.那你應該付34元.
小明:我把兩種文具的單價弄反了,以為要付46元.
(1)求小明所購買的黑色水筆和筆記本的單價;
(2)如果小紅也去購買同樣的黑色水筆和筆記本,預算費用不超過88元,并且購買筆記本的數量要比購買黑色水筆的數量多1,那么小紅最多能購買多少本筆記本?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知OM⊥ON,垂足為O,點A、B分別是射線OM、ON上的一點(O點除外).

(1)如圖①,射線AC平分∠OAB,若BC所在的直線也平分以B為頂點的某一個角α(0°<α<180°),則∠ACB= ;
(2)如圖②,P為平面上一點(O點除外),∠APB=90°,且OA≠AP,分別畫∠OAP、∠OBP的平分線AD、BE,交BP、OA于點D、E,試判斷AD與BE的位置關系,并說明理由;
(3)在(2)的條件下,隨著P點在平面內運動,AD、BE的位置關系是否發生變化?請利用圖③畫圖探究.如果不變,直接回答;如果變化,畫出圖形,寫出AD、BE位置關系并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com