
【題目】在同一直角坐標系中,直線y=﹣x+3與y=3x﹣5相交于C點,分別與x軸交于A、B兩點.P、Q分別為直線y=﹣x+3與y=3x﹣5上的點.
(1)求△ABC的面積;
(2)若P、Q關于原點成中心對稱,求P點的坐標;
(3)若△QPC≌△ABC,求Q點的坐標.
【答案】
(1)
解:依照題意畫出圖形,如圖1所示.
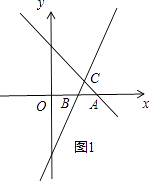
令y=﹣x+3中y=0,則x=3,
∴A(3,0);
令y=3x﹣5中y=0,則x= ![]() ,
,
∴B( ![]() ,0);
,0);
聯立兩直線解析式成方程組,得: ![]() ,解得:
,解得: ![]() ,
,
∴C(2,1).
S△ABC= ![]() AByC=
AByC= ![]() (3﹣
(3﹣ ![]() )×1=
)×1= ![]()
(2)
解:∵點P在直線y=﹣x+3上,
∴設P(m,﹣m+3),
∵P、Q關于原點成中心對稱,
∴Q(﹣m,m﹣3).
∵點Q在直線y=3x﹣5上,
∴m﹣3=﹣3m﹣5,
解得:m=﹣ ![]() ,
,
∴點P的坐標為(﹣ ![]() ,
, ![]() )
)
(3)
解:依照題意畫出圖形,如圖2所示.
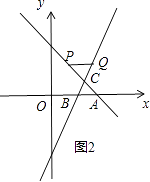
若要△QPC≌△ABC,只需PQ∥AB,且PQ=AB即可.
設P(3﹣n,n),則Q( ![]() ,n),
,n),
∵PQ=AB,
∴ ![]() ﹣(3﹣n)=3﹣
﹣(3﹣n)=3﹣ ![]() ,
,
解得:n=2,
∴點Q( ![]() ,2).
,2).
【解析】(1)分別令y=﹣x+3與y=3x﹣5中y=0求出x值,即可得出點A、B的坐標,聯立兩直線解析式成方程組,解方程組即可求出點C的坐標,再結合三角形的面積公式即可求出△ABC的面積;(2)由點P在直線y=﹣x+3上,設點P(m,﹣m+3),由P、Q關于原點對稱,由此可找出Q(﹣m,m﹣3),由點Q的坐標利用一次函數圖象上點的坐標特征即可找出關于m的一元一次方程,解方程求出m值,將其代入點P的坐標中即可得出結論;(3)由△QPC≌△ABC可得出PQ∥AB,且PQ=AB,設P(3﹣n,n),則Q( ![]() ,n),再由PQ=AB即可得出關于n的一元一次方程,解方程即可求出n值,將其代入點Q的坐標中,即可得出結論.
,n),再由PQ=AB即可得出關于n的一元一次方程,解方程即可求出n值,將其代入點Q的坐標中,即可得出結論.


科目:初中數學 來源: 題型:
【題目】某電腦公司銷售部為了定制下個月的銷售計劃,對20位銷售員本月的銷售量進行了統計,繪制成如圖所示的統計圖,則這20位銷售人員本月銷售量的平均數、中位數、眾數分別是( ) 
A.19,20,14
B.19,20,20
C.18.4,20,20
D.18.4,25,20
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B的坐標分別為(1,4)和(4,4),拋物線y=a(x+m)2+n的頂點在線段AB上,與x軸交于C,D兩點(C在D的左側),點C的橫坐標最小值為﹣3,則點D的橫坐標的最大值為 . 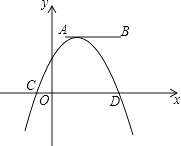
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義{a,b,c}為函數y=ax2+bx+c的“特征數”.
(1)“特征數”為{﹣1,2,3}的函數解析式為 , 將“特征數”為{0,1,1}的函數向下平移兩個單位以后得到的函數解析式為;
(2)我們把橫、縱坐標均為整數的點稱為“整點”,試問:在上述兩空填寫的函數圖象圍成的封閉圖形(包含邊界)內共有多少個整點?請給出詳細的運算過程;
(3)定義“特征數”的運算:①{a1 , b1 , c1}+{a2 , b2 , c2}={a1+a2 , b1+b2 , c1+c2};②λ{a1 , b1 , c1}={λa1 , λb1 , λc1}(其中λ為任意常數).試問:“特征數”為{﹣1,2,3}+λ{0,1,﹣1}的函數是否過定點?如果過定點,請計算出該定點坐標;如果不存在,請說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半圓O的直徑,點C在半圓O上,AB=5cm,AC=4cm.D是弧BC上的一個動點(含端點B,不含端點C),連接AD,過點C作CE⊥AD于E,連接BE,在點D移動的過程中,BE的取值范圍是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,Rt△ABC中,∠ABC=90°,AD平分∠BAC交BC于D. 
(1)用尺規畫圓O,使圓O過A、D兩點,且圓心O在邊AC上.(保留作圖痕跡,不寫作法)
(2)求證:BC與圓O相切;
(3)設圓O交AB于點E,若AE=2,CD=2BD.求線段BE的長和弧DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,BC=AC=2,D是斜邊AB上一個動點,把△ACD沿直線CD折疊,點A落在同一平面內的A′處,當A′D平行于Rt△ABC的直角邊時,AD的長為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l:y=kx+b(k≠0)的圖象與x軸、y軸交于A、B兩點,A(﹣2,0),B(0,1).
(1)求直線l的函數表達式;
(2)若P是x軸上的一個動點,請直接寫出當△PAB是等腰三角形時P的坐標;
(3)在y軸上有點C(0,3),點D在直線l上,若△ACD面積等于4,求點D的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD為等腰梯形,AD∥BC,AB=CD,AD= ![]() ,E為CD中點,連接AE,且AE=2
,E為CD中點,連接AE,且AE=2 ![]() ,∠DAE=30°,作AE⊥AF交BC于F,則BF=( )
,∠DAE=30°,作AE⊥AF交BC于F,則BF=( ) 
A.1
B.3﹣ ![]()
C.![]() ﹣1
﹣1
D.4﹣2 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com