
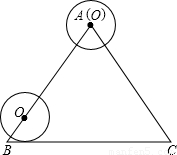
 -BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.
-BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.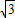 厘米,求⊙O首次與BC邊相切時,AO的長.
厘米,求⊙O首次與BC邊相切時,AO的長.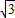 .
.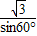 =2.
=2.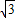 厘米.
厘米.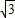 厘米時,⊙O在移動中與△ABC的邊共相切三次,即切點個數為3;
厘米時,⊙O在移動中與△ABC的邊共相切三次,即切點個數為3;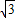 時,⊙O在移動中與△ABC的邊相切六次,即切點個數為6;
時,⊙O在移動中與△ABC的邊相切六次,即切點個數為6;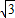 時,⊙O與△ABC不能相切,即切點個數為0.
時,⊙O與△ABC不能相切,即切點個數為0.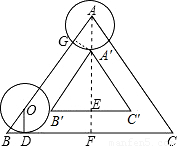
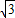 -3r,
-3r,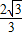 A′E=2
A′E=2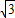 (
(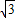 -r).
-r). B′C′•A′E=3
B′C′•A′E=3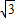 (
(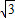 -r)2.
-r)2.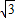 (
(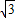 -r)2(0<r<3).
-r)2(0<r<3).

 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源:2002年全國中考數學試題匯編《銳角三角函數》(04)(解析版) 題型:解答題
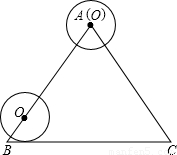 -BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.
-BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.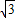 厘米,求⊙O首次與BC邊相切時,AO的長.
厘米,求⊙O首次與BC邊相切時,AO的長.查看答案和解析>>
科目:初中數學 來源:2002年全國中考數學試題匯編《圓》(11)(解析版) 題型:解答題
 -BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.
-BC-CA運動,回到點A時,⊙O隨著點O的運動而移動. 厘米,求⊙O首次與BC邊相切時,AO的長.
厘米,求⊙O首次與BC邊相切時,AO的長.查看答案和解析>>
科目:初中數學 來源:2002年全國中考數學試題匯編《三角形》(09)(解析版) 題型:解答題
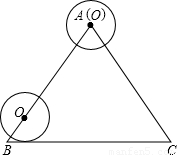 -BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.
-BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.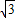 厘米,求⊙O首次與BC邊相切時,AO的長.
厘米,求⊙O首次與BC邊相切時,AO的長.查看答案和解析>>
科目:初中數學 來源:2002年江西省中考數學試卷(解析版) 題型:解答題
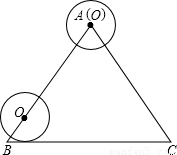 -BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.
-BC-CA運動,回到點A時,⊙O隨著點O的運動而移動.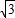 厘米,求⊙O首次與BC邊相切時,AO的長.
厘米,求⊙O首次與BC邊相切時,AO的長.查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com