
【題目】對于有理數a,b,定義一種新運算“⊙”,規定a⊙b=|a+b|+|a﹣b|.
![]()
(1)計算2⊙(﹣3)的值;
(2)當a,b在數軸上的位置如圖所示時,化簡a⊙b;
(3)已知(a⊙a)⊙a=8+a,求a的值.
【答案】(1)2⊙(﹣3)=6;(2)a⊙b=﹣2b;(3)當a≥0時, a=![]() ;當a<0時, a=﹣
;當a<0時, a=﹣![]() .
.
【解析】
(1)根據文中的新運算法則將2⊙(﹣3)轉化為我們熟悉的計算方式進行計算即可;
(2)根據文中的新運算法則將a⊙b轉化為|a+b|+|a﹣b|,然后先判斷出a+b與a﹣b的正負性,之后利用絕對值代數意義化簡即可;
(3)先根據文中的新運算法則將(a⊙a)⊙a轉化為我們熟悉的計算方式,此時注意對a進行分a≥0、a<0兩種情況討論,然后得出新的方程求解即可.
(1)由題意可得:2⊙(﹣3)=|2﹣3|+|2+3|=6;
(2)由數軸可知,a+b<0,a﹣b>0,
∴a⊙b=|a+b|+|a﹣b|=﹣a﹣b+a﹣b=﹣2b;
(3)當a≥0時,(a⊙a)⊙a=2a⊙a=4a=8+a,
∴a=![]() ;
;
當a<0時,(a⊙a)⊙a=(﹣2a)⊙a=﹣4a=8+a,
∴a=![]() .
.
綜上所述,a的值為![]() 或
或![]() .
.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:
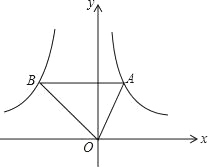
【題目】如圖,點A是反比例函數y1=![]() (x>0)圖象上的任意一點,過點A作 AB∥x軸,交另一個比例函數y2=
(x>0)圖象上的任意一點,過點A作 AB∥x軸,交另一個比例函數y2=![]() (k<0,x<0)的圖象于點B.
(k<0,x<0)的圖象于點B.
(1)若S△AOB的面積等于3,則k是=_____;
(2)當k=﹣8時,若點A的橫坐標是1,求∠AOB的度數;
(3)若不論點A在何處,反比例函數y2=![]() (k<0,x<0)圖象上總存在一點D,使得四邊形AOBD為平行四邊形,求k的值.
(k<0,x<0)圖象上總存在一點D,使得四邊形AOBD為平行四邊形,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合實踐
問題情景:某綜合實踐小組進行廢物再利用的環保小衛士行動. 他們準備用廢棄的宣傳單制作裝垃圾的無蓋紙盒.
操作探究:
⑴若準備制作一個無蓋的正方體形紙盒,如圖1,下面的哪個圖形經過折疊能圍成無蓋正方體形紙盒?

⑵如圖2是小明的設計圖,把它折成無蓋正方體形紙盒后與“保”字相對的是哪個字?
⑶如圖3,有一張邊長為20cm的正方形廢棄宣傳單,小華準備將其四角各剪去一個小正方形,折成無蓋長方體形紙盒.
①請你在圖3中畫出示意圖,用實線表示剪切線,虛線表示折痕.
②若四角各剪去了一個邊長為xcm的小正方形,用含x的代數式表示這個紙盒的高為 cm,底面積為 cm2,當小正方形邊長為4cm時,紙盒的容積為 cm3.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數填入表示它所在的數集的括號里
﹣(﹣2.3),![]() ,0,﹣
,0,﹣![]() ,30%,π,﹣|﹣2013|,﹣5
,30%,π,﹣|﹣2013|,﹣5![]() ,
,![]()
(1)負整數集合[ …]
(2)正有理數集合[ …]
(3)分數集合[ …]
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=8,BC=6。P是AB邊上的一個動點(異于A、B兩點),過點P分別作AC、BC邊的垂線,垂足為M、N設AP=x。

(1)在△ABC中,AB= ;
(2)當x= 時,矩形PMCN的周長是14;
(3)是否存在x的值,使得△PAM的面積、△PBN的面積與矩形PMCN的面積同時相等?請說出你的判斷,并加以說明。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt∠AOB的平分線ON上依次取點C,F,M,過點C作DE⊥OC,分別交OA,OB于點D,E,以FM為對角線作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,設OC=x,圖中陰影部分面積為y,則y與x之間的函數關系式是( )
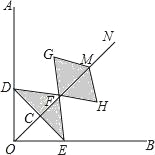
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A=a2﹣2b2+2ab﹣3,B=2a2﹣b2﹣![]() ab﹣
ab﹣![]() .
.
(1)求2(A+B)﹣3(2A﹣B)的值(結果用化簡后的a、b的式子表示);
(2)當![]() 與b2互為相反數時,求(1)中式子的值.
與b2互為相反數時,求(1)中式子的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年“十一”黃金周期間,某風景區在7天假期中每天旅游的人數變化如下表(正數表示比前一天多的人數,負數表示比前一天少的人數,單位:萬人),已知9月30日的游客人數為0.3萬人,請回答下列問題:
日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人數變化 | +1.8 | +0.8 | +0.2 | -0.4 | -0.8 | +0.2 | -1.0 |
(1)七天內游客人數最多的是 日,最少的是 日;
(2)若以9月30日的游客人數為0點,用折線統計圖表示這7天的游客人數變化情況?
(3)求這7天的游客人數是多少萬人.
查看答案和解析>>
科目:初中數學 來源: 題型:
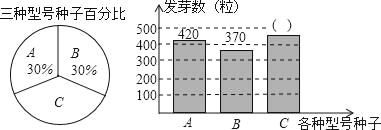
【題目】松山區種子培育基地用A,B,C三種型號的甜玉米種子共1500粒進行發芽試驗,從中選出發芽率高的種子進行推廣,通過試驗知道,C型號種子的發芽率為80%,根據試驗數據繪制了下面兩個不完整的統計圖:
(1)求C型號種子的發芽數;
(2)通過計算說明,應選哪種型號的種子進行推廣?
(3)如果將所有已發芽的種子放在一起,從中隨機取出一粒,求取到C型號發芽種子的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com