
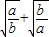 的值.
的值.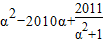 的值.
的值. =2011,然后整體代入原式,求出
=2011,然后整體代入原式,求出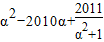 的值.
的值.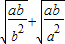
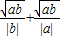
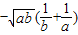
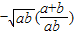
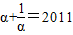 .
.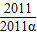 =
=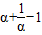 =2010.
=2010.

科目:初中數學 來源: 題型:
 4、如圖為某班35名學生在某次社會實踐活動中揀廢棄的礦泉水瓶情況條形統計圖,圖中上面部分數據破損導致數據不完全.已知此次活動中學生揀到礦泉水瓶個數中位數是5個,則根據統計圖,下列選項中的( )數值無法確定.
4、如圖為某班35名學生在某次社會實踐活動中揀廢棄的礦泉水瓶情況條形統計圖,圖中上面部分數據破損導致數據不完全.已知此次活動中學生揀到礦泉水瓶個數中位數是5個,則根據統計圖,下列選項中的( )數值無法確定.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com