
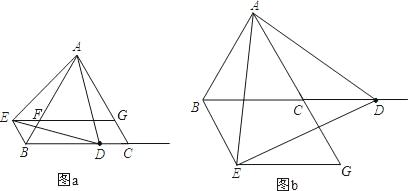
【題目】△ABC是等邊三角形,點D是射線BC上的一個動點(點D不與點B、C重合),△ADE是以AD為邊的等邊三角形,過點E作BC的平行線,分別交射線AB、AC于點F、G,連接BE.
(1)如圖(a)所示,當點D在線段BC上時.
①求證:△AEB≌△ADC;
②探究四邊形BCGE是怎樣特殊的四邊形?并說明理由;
(2)如圖(b)所示,當點D在BC的延長線上時,直接寫出(1)中的兩個結論是否成立;
(3)在(2)的情況下,當點D運動到什么位置時,四邊形BCGE是菱形?并說明理由.
【答案】(1)①見解析,②四邊形BCGE是平行四邊形,見解析;(2)①②都成立;(3)當CD=CB (∠CAD=30°或∠BAD=90°或∠ADC=30°)時,四邊形BCGE是菱形,見解析.
【解析】
(1)根據等邊三角形的性質可得AB=AC,AE=AD,∠BAC=∠EAD=60°,然后求出∠BAE=∠CAD,再利用“邊角邊”證明△AEB和△ADC全等;②四邊形BCGE是平行四邊形,因為△AEB≌△ADC,所以可得∠ABE=∠C=60°,進而證明∠ABE=∠BAC,則可得到EB∥GC又EG∥BC,所以四邊形BCGE是平行四邊形;
(2)根據(1)的思路解答即可.(3)當CD=CB時,四邊形BCGE是菱形,由(1)可知△AEB≌△ADC,可得BE=CD,再證明BE=CB,即鄰邊相等的平行四邊形是菱形.
證明:(1)①∵△ABC和△ADE都是等邊三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°.
又∵∠EAB=∠EAD﹣∠BAD,∠DAC=∠BAC﹣∠BAD,
∴∠EAB=∠DAC,
∴△AEB≌△ADC(SAS).
②方法一:由①得△AEB≌△ADC,
∴∠ABE=∠C=60°.
又∵∠BAC=∠C=60°,
∴∠ABE=∠BAC,
∴EB∥GC.
又∵EG∥BC,
∴四邊形BCGE是平行四邊形.
方法二:證出△AEG≌△ADB,得EG=AB=BC.
∵EG∥BC,
∴四邊形BCGE是平行四邊形.
(2)①②都成立.
(3)當CD=CB (∠CAD=30°或∠BAD=90°或∠ADC=30°)時,四邊形BCGE是菱形.
理由:方法一:由①得△AEB≌△ADC,
∴BE=CD
又∵CD=CB,
∴BE=CB.
由②得四邊形BCGE是平行四邊形,
∴四邊形BCGE是菱形.
方法二:由①得△AEB≌△ADC,
∴BE=CD.
又∵四邊形BCGE是菱形,
∴BE=CB
∴CD=CB.
方法三:∵四邊形BCGE是平行四邊形,
∴BE∥CG,EG∥BC,
∴∠FBE=∠BAC=60°,∠F=∠ABC=60°
∴∠F=∠FBE=60°,∴△BEF是等邊三角形.
又∵AB=BC,四邊形BCGE是菱形,
∴AB=BE=BF,
∴AE⊥FG
∴∠EAG=30°,
∵∠EAD=60°,
∴∠CAD=30°.


科目:初中數學 來源: 題型:
【題目】已知y是x的一次函數,當x=1時,y=1;當x=-2時,y=-14.
(1)求這個一次函數的關系式;
(2)在如圖所示的平面直角坐標系中作出函數的圖像;
(3)由圖像觀察,當0≤x≤2時,函數y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
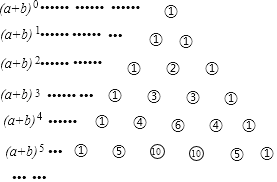
【題目】我國古代數學的許多創新和發展都位居世界前列,如南宋數學家楊輝(約13世紀)所著的《詳解九章算術》一書中,用如下的三角形解釋(a+b)n的展開式中各項的系數,此三角形稱為“楊輝三角”,
即:(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
根據“楊輝三角”計算出(a+b)10的展開式中第三項的系數為( )
A.10B.45C.46D.50
查看答案和解析>>
科目:初中數學 來源: 題型:
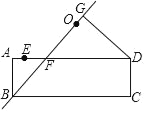
【題目】如圖,矩形ABCD中,AB=3,AD=9,點E在邊AD上,AE=1,過E、D兩點的圓的圓心O在邊AD的上方,直線BO交AD于點F,作DG⊥BO,垂足為G.當△ABF與△DFG全等時,⊙O的半徑為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小宇想測量位于池塘兩端的A,B兩點的距離.他沿著與直線AB平行的道路EF行走,當行走到點C處,測得∠ACF=45°,再向前行走100米到點D處,測得∠BDF=60°.若直線AB與EF之間的距離為60米,求A,B兩點的距離.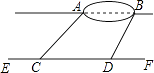
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠BAC=90°,點D是BC上一點,將△ABD沿AD翻折后得到△AED,邊AE交BC于點F.


(1)如圖①,當AE⊥BC時,寫出圖中所有與∠B相等的角: ;所有與∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度數;
②是否存在這樣的x的值,使得△DEF中有兩個角相等.若存在,并求x的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:已知方程a2![]() 2a
2a![]() 1=0,1
1=0,1![]() 2b
2b![]() b2=0且ab≠1,求
b2=0且ab≠1,求![]() 的值.
的值.
解:由a2![]() 2a
2a![]() 1=0及1
1=0及1![]() 2b
2b![]() b2=0,
b2=0,
可知a≠0,b≠0,
又∵ab≠1,![]() .
.
1![]() 2b
2b![]() b2=0可變形為
b2=0可變形為
![]() ,
,
根據a2![]() 2a
2a![]() 1=0和
1=0和![]() 的特征.
的特征.
![]() 、
、![]() 是方程x2
是方程x2![]() 2x
2x![]() 1=0的兩個不相等的實數根,
1=0的兩個不相等的實數根,
則![]() ,即
,即![]() .
.
根據閱讀材料所提供的方法,完成下面的解答.
已知:3m2![]() 7m
7m![]() 2=0,2n2+7n
2=0,2n2+7n![]() 3=0且mn≠1,求
3=0且mn≠1,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com