
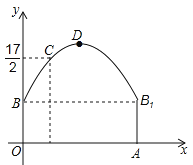
【題目】(12分)如圖所示是隧道的截面由拋物線和長方形構成,長方形的長是12 m,寬是4 m.按照圖中所示的直角坐標系,拋物線可以用y=![]() x2+bx+c表示,且拋物線上的點C到OB的水平距離為3 m,到地面OA的距離為
x2+bx+c表示,且拋物線上的點C到OB的水平距離為3 m,到地面OA的距離為![]() m.
m.
(1)求拋物線的函數關系式,并計算出拱頂D到地面OA的距離;
(2)一輛貨運汽車載一長方體集裝箱后高為6m,寬為4m,如果隧道內設雙向車道,那么這輛貨車能否安全通過?
(3)在拋物線型拱壁上需要安裝兩排燈,使它們離地面的高度相等,如果燈離地面的高度不超過8m,那么兩排燈的水平距離最小是多少米?
【答案】(1)拋物線的函數關系式為y=![]() x2+2x+4,拱頂D到地面OA的距離為10 m;(2)兩排燈的水平距離最小是4
x2+2x+4,拱頂D到地面OA的距離為10 m;(2)兩排燈的水平距離最小是4![]() m.
m.
【解析】
試題根據點B和點C在函數圖象上,利用待定系數法求出b和c的值,從而得出函數解析式,根據解析式求出頂點坐標,得出最大值;根據題意得出車最外側與地面OA的交點為(2,0)(或(10,0)),然后求出當x=2或x=10時y的值,與6進行比較大小,比6大就可以通過,比6小就不能通過;將y=8代入函數,得出x的值,然后進行做差得出最小值.
試題解析:(1)由題知點![]() 在拋物線上
在拋物線上
所以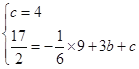 ,解得
,解得![]() ,所以
,所以![]()
所以,當![]() 時,
時,![]()
答:![]() ,拱頂D到地面OA的距離為10米
,拱頂D到地面OA的距離為10米
(2)由題知車最外側與地面OA的交點為(2,0)(或(10,0))
當![]() 時,
時,![]() ,所以可以通過
,所以可以通過
(3)令![]() ,即
,即![]() ,可得
,可得![]() ,解得
,解得![]()
![]() 答:兩排燈的水平距離最小是
答:兩排燈的水平距離最小是![]()


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,AC=10,點O在AC上,且AO=3,點P是AB上一動點,連結OP,將線段OP繞點O逆時針旋轉60°得到線段OD.要使點D恰好落在BC上,則AP的長是 ( )
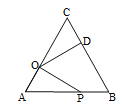
A. 5B. 6C. 7D. 9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】股民李金上星期六買進某公司的股票,每股![]() 元,下表為本周內該股票的漲跌情況:
元,下表為本周內該股票的漲跌情況:
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
每股漲跌(與前一天相比) |
|
|
|
|
|
|
星期三收盤時,每股是________元;本周內最高價是每股________元, 最低價是每股______元.
查看答案和解析>>
科目:初中數學 來源: 題型:
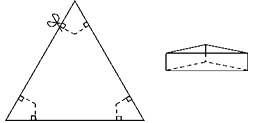
【題目】如圖,以邊長為20cm的正三角形紙板的各頂點為端點,在各邊上分別截取4cm長的六條線段,過截得的六個端點作所在邊的垂線,形成三個有兩個直角的四邊形.把它們沿圖中 虛線剪掉,用剩下的紙板折成一個底為正三角形的無蓋柱形盒子,則它的容積為________cm3 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】4月23日是“世界讀書日”,學校開展“讓書香溢滿校園”讀書活動,以提升青少年的閱讀興趣,九年級(1)班數學活動小組對本年級600名學生每天閱讀時間進行了統計,根據所得數據繪制了兩幅不完整統計圖(每組包括最小值不包括最大值).九年級(1)班每天閱讀時間在0.5小時以內的學生占全班人數的8%.根據統計圖解答下列問題:
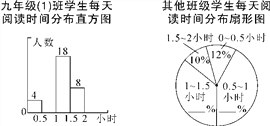
(1)九年級(1)班有 名學生;
(2)補全直方圖;
(3)除九年級(1)班外,九年級其他班級每天閱讀時間在1~1.5小時的學生有165人,請你補全扇形統計圖;
(4)求該年級每天閱讀時間不少于1小時的學生有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以下四組條件中,無法判定△ABC≌△DEF的是( )
A. AB=DE,BC=EF,∠B=∠EB. ∠B=∠E,BC=EF,∠C=∠F
C. ∠B=∠E,∠A=∠D,BC=EFD. AB=DE,BC=EF,∠C=∠D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】7張如圖1的長為a,寬為b(a>b)的小長方形紙片,按圖2的方式不重疊地放在矩形ABCD內,未被覆蓋的部分(兩個矩形)用陰影表示.設左上角與右下角的陰影部分的面積的差為S,當BC的長度變化時,按照同樣的放置方式,S始終保持不變,則a,b滿足( )
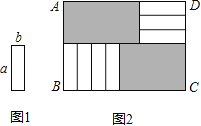
A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
查看答案和解析>>
科目:初中數學 來源: 題型:
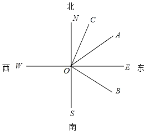
【題目】如圖,直線SN為南北方向,OB的方向是南偏東60°,∠SOB與∠NOC互余,OA平分∠BON.
(1)射線OC的方向是 .
(2)求∠AOC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com