
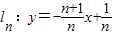 (n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線
(n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線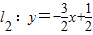 與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2,…,
與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2,…,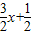 ,所以分別令y=0,x=0即可求出A2(
,所以分別令y=0,x=0即可求出A2( ,0),同理可求出A2,A3…所以推出當n=n時,yn=
,0),同理可求出A2,A3…所以推出當n=n時,yn=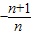 x+
x+ ,分別令y=0,x=0,即可求出An(
,分別令y=0,x=0,即可求出An(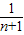 ,0),Bn(0,
,0),Bn(0,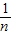 ),所以Sn=
),所以Sn= ,整理即可求出答案.
,整理即可求出答案. ,0),B1(0,1),
,0),B1(0,1),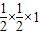 =
= ;
;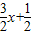 ,
, ,0),B2(0,
,0),B2(0, )
) ,
,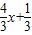 ,
, ,0),B3(0,
,0),B3(0, ),
),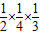 ,
,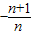 x+
x+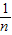 ,
,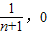 ),Bn(0,
),Bn(0,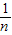 ),
),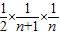 ,
,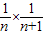 =
= ,
, (
(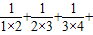 …
…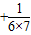 )
) [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(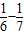 )]=
)]= (1-
(1- )=
)= .
.

科目:初中數學 來源: 題型:解答題
 (n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線
(n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線 與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2,…,
與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2,…,查看答案和解析>>
科目:初中數學 來源:2008-2009學年重慶市一中九年級(上)期末數學試卷(解析版) 題型:填空題
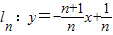 (n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線
(n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線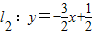 與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2;…依此類推,直線ln與x軸和y軸分別交于點An和Bn,S1+S2+…+S2009的值是 .
與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2;…依此類推,直線ln與x軸和y軸分別交于點An和Bn,S1+S2+…+S2009的值是 .查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《一次函數》(06)(解析版) 題型:解答題
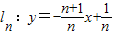 (n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線
(n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線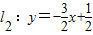 與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2,…,
與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2,…,查看答案和解析>>
科目:初中數學 來源:2009年浙江省溫州市樂清中學保送生綜合素質測試數學試卷(解析版) 題型:解答題
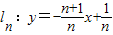 (n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線
(n是不為零的自然數).當n=1時,直線l1:y=-2x+1與x軸和y軸分別交于點A1和B1,設△A1OB1(其中O是平面直角坐標系的原點)的面積為S1;當n=2時,直線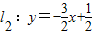 與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2,…,
與x軸和y軸分別交于點A2和B2,設△A2OB2的面積為S2,…,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com