
【題目】如圖,BE,CE平分△ABC的兩個外角,且交于點E,∠A=80°.
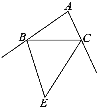
(1)∠E的度數是多少?
(2)若∠ABC=35°,寫出四邊形ABEC各內角的度數.
【答案】(1)∠E=50°;(2)四邊形ABEC各內角的度數為∠A=80°,∠ABE=107.5°,∠E=50°,∠ACE=122.5°.
【解析】
(1)由BE、CE是兩外角的平分線,得到![]() 根據三角形的外角的性質和三角形的內角和得到
根據三角形的外角的性質和三角形的內角和得到![]() +∠ABC)=180°,于是得到
+∠ABC)=180°,于是得到![]() 即可得到結論;
即可得到結論;
(2)由∠ABC=35°,根據鄰補角的定義得到∠DBC=180°-∠ABC=145°,由BE平分∠DBC,得到![]() ,于是得到
,于是得到![]() ,于是得到
,于是得到![]() ,然后根據四邊形的內角和得到結果.
,然后根據四邊形的內角和得到結果.
解:(1)如圖.∵BE,CE平分△ABC的兩個外角,
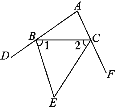
∴∠1=![]() ∠CBD,∠2=
∠CBD,∠2=![]() ∠BCF.
∠BCF.
∵∠CBD=∠A+∠ACB,∠BCF=∠A+∠ABC,
∴∠1=![]() (∠A+∠ACB),∠2=
(∠A+∠ACB),∠2=![]() (∠A+∠ABC).
(∠A+∠ABC).
∵∠E+∠1+∠2=180°,
∴∠E+![]() (∠A+∠ACB)+
(∠A+∠ACB)+![]() (∠A+∠ABC)=180°,
(∠A+∠ABC)=180°,
即∠E+![]() ∠A+
∠A+![]() (∠A+∠ACB+∠ABC)=180°.
(∠A+∠ACB+∠ABC)=180°.
∵∠A+∠ACB+∠ABC=180°,∴∠E+![]() ∠A=90°,
∠A=90°,
∴∠E=90°-![]() ∠A=50°.
∠A=50°.
(2)∵∠ABC=35°,∴∠CBD=180°-∠ABC=145°.
∵BE平分∠CBD,∴∠1=72.5°,
∴∠ABE=35°+72.5°=107.5°,
∴∠ACE=360°-∠A-∠E-∠ABE=122.5°,
∴四邊形ABEC各內角的度數為:∠A=80°,
∠ABE=107.5°,∠E=50°,∠ACE=122.5°.


科目:初中數學 來源: 題型:
【題目】如圖,直線m∥n,Rt△ABC的頂點A在直線n上,∠C=90°,AB,CB分別交直線m于點D和點E,且DB=DE,若∠1=65°,則∠BDE的度數為( )
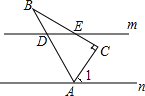
A.115°B.120°C.130°D.145°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】設a,b是任意兩個不等實數,我們規定:滿足不等式a≤x≤b的實數x的所有取值的全體叫做閉區間,表示為[a,b].對于一個函數,如果它的自變量x與函數值y滿足:當m≤x≤n時,有m≤y≤n,我們就稱此函數是閉區間[m,n]上的“閉函數”.如函數y=﹣x+4,當x=1時,y=3;當x=3時,y=1,即當1≤x≤3時,恒有1≤y≤3,所以說函數y=﹣x+4是閉區間[1,3]上的“閉函數”,同理函數y=x也是閉區間[1,3]上的“閉函數”.
(1)反比例函數y=![]() 是閉區間[1,2018]上的“閉函數”嗎?請判斷并說明理由;
是閉區間[1,2018]上的“閉函數”嗎?請判斷并說明理由;
(2)如果已知二次函數y=x2﹣4x+k是閉區間[2,t]上的“閉函數”,求k和t的值;
(3)如果(2)所述的二次函數的圖象交y軸于C點,A為此二次函數圖象的頂點,B為直線x=1上的一點,當△ABC為直角三角形時,寫出點B的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按下面的程序計算:當輸入x=100 時,輸出結果是299;當輸入x=50時,輸出結果是446;如果輸入 x 的值是正整數,輸出結果是257,那么滿足條件的x的值最多有( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某路燈在鉛垂面內的示意圖,燈柱AC的高為11米,燈桿AB與燈柱AC的夾角∠A=120°,路燈采用錐形燈罩,在地面上的照射區域DE長為18米,從D,E兩處測得路燈B的仰角分別為α和β,且tanα=6,tanβ=![]() ,求燈桿AB的長度.
,求燈桿AB的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以AB為直徑的⊙O的圓心O到直線l的距離OE=3,⊙O的半徑r=2,直線AB不垂直于直線l,過點A,B分別作直線l的垂線,垂足分別為點D,C,則四邊形ABCD的面積的最大值為__________.
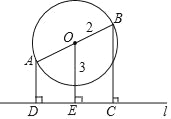
查看答案和解析>>
科目:初中數學 來源: 題型:
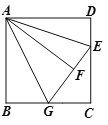
【題目】如圖,在正方形ABCD中,AB=3,點E在CD邊上,且CE=2DE,將△ADE沿直線AE對折至△AEF,延長EF交BC于G,連接AG,則線段AG的長為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com