(1)第26屆世界大學生夏季運動會將在深圳舉行,為了宣傳“低碳大運、綠色大運”理念,在倒計時一百天當日,組委會組織了長跑隊和自行車隊進行理念宣傳活動,全程共10千米,自行車隊的速度是長跑隊速度的2.5倍,自行車隊出發半小時后,長跑隊才出發,結果長跑隊比自行車隊晚2小時到達終點,求長跑隊跑步和自行車隊騎行的速度各是多少?
(2)在活動的終點處,組委會為活動參與者準備了若干箱紀念品,由工作人員負責發放,若每名工作人員分發3箱,則剩余4箱紀念品,若前面每名工作人員負責發4箱,則最后一名工作人員負責分發的紀念品不足3箱,求工作人員人數及紀念品的箱數各是多少?
解:(1)設長跑隊的速度為x千米/時,則自行車隊的速度是2.5x千米/時,
則長跑隊用時
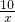
,自行車隊用時
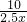
,
由題意得:
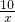
-
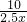
=2-0.5,
解得:x=4,則2.5x=10.
即長跑隊的速度為4千米/時,自行車隊的速度為10千米/時.
(2)設工作人員y人,則紀念品的箱數為3y+4,
由題意得:0≤3y+4-4(y-1)<3,
解得:5<y≤8,
①當人數y=6時,紀念品箱數為22;
②當人數y=7時,紀念品箱數為25;
③當人數y=8時,紀念品箱數為28;
答:工作人員為6,紀念品箱數為22,或工作人員為7,紀念品箱數為25,或工作人員為8,紀念品箱數為28.
分析:(1)設長跑隊的速度為x千米/小時,則自行車隊的速度是2.5x千米/小時,根據長跑隊比自行車隊晚2小時到達終點可列出方程,解出即可.
(2)設工作人員y人,則紀念品的箱數為3y+4,然后根據每名工作人員發4箱,最后一名工作人員負責分發的紀念品不足3箱可得出不等式組,解出后討論y的值即可.
點評:本題考查了分式方程的應用及一元一次不等式組的應用,兩者結合著進行考察,比較新穎,注意審題,得出等量關系及不等關系是解答本題的關鍵.

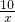 ,自行車隊用時
,自行車隊用時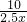 ,
,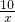 -
-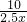 =2-0.5,
=2-0.5,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案