
【題目】已知:OB、OC、OE是∠AOD內的射線,若∠AOD=130°.
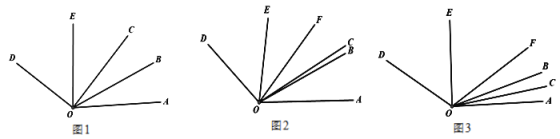
(1)如圖1,OB是∠AOC的平分線,OE是∠COD的平分線,∠BOE=_____度;
(2)OF也是∠AOD內的射線,如圖2,若∠FOC=20°,OB平分∠AOF,OE平分∠COD,當射線OC繞點O在∠AOF內旋轉時,求∠BOE的大小;
(3)在(2)的條件下,當射線OC從邊OA開始繞O點以每秒2°的速度逆時針旋轉t秒,如圖3,若∠AOB:∠DOE=2:3,求t的值.
科目:初中數學 來源: 題型:
【題目】2013年1月1日新交通法規開始實施.為了解某社區居民遵守交通法規情況,小明隨機選取部分居民就“行人闖紅燈現象”進行問卷調查,調查分為“A:從不闖紅燈;B:偶爾闖紅燈;C:經常闖紅燈;D:其他”四種情況,并根據調查結果繪制出部分條形統計圖(如圖1)和部分扇形統計圖(如圖2).請根據圖中信息,解答下列問題:
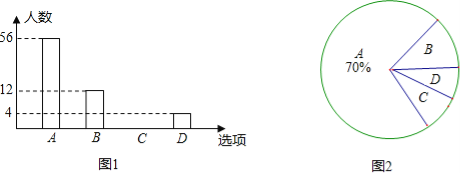
(1)本次調查共選取 名居民;
(2)求出扇形統計圖中“C”所對扇形的圓心角的度數,并將條形統計圖補充完整;
(3)如果該社區共有居民1600人,估計有多少人從不闖紅燈?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七(1)班的學習小組學習“線段中點”內容時,得到一個很有意思的結論,請跟隨他們一起思考.
(1)發現:
如圖1,線段![]() ,點
,點![]() 在線段
在線段![]() 上,當點
上,當點![]() 是線段
是線段![]() 和線段
和線段![]() 的中點時,線段
的中點時,線段![]() 的長為_________;若點
的長為_________;若點![]() 在線段
在線段![]() 的延長線上,其他條件不變(請在圖2中按題目要求將圖補充完整),得到的線段
的延長線上,其他條件不變(請在圖2中按題目要求將圖補充完整),得到的線段![]() 與線段
與線段![]() 之間的數量關系為_________.
之間的數量關系為_________.
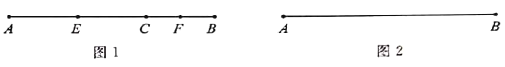
(2)應用:
如圖3,現有長為40米的拔河比賽專用繩![]() ,其左右兩端各有一段(
,其左右兩端各有一段(![]() 和
和![]() )磨損了,磨損后的麻繩不再符合比賽要求. 已知磨損的麻繩總長度不足20米. 小明認為只利用麻繩
)磨損了,磨損后的麻繩不再符合比賽要求. 已知磨損的麻繩總長度不足20米. 小明認為只利用麻繩![]() 和一把剪刀(剪刀只用于剪斷麻繩)就可以得到一條長20米的拔河比賽專用繩
和一把剪刀(剪刀只用于剪斷麻繩)就可以得到一條長20米的拔河比賽專用繩![]() . 小明所在學習小組認為此法可行,于是他們應用“線段中點”的結論很快做出了符合要求的專用繩
. 小明所在學習小組認為此法可行,于是他們應用“線段中點”的結論很快做出了符合要求的專用繩![]() ,請你嘗試著“復原”他們的做法:
,請你嘗試著“復原”他們的做法:
①在圖中標出點![]() 、點
、點![]() 的位置,并簡述畫圖方法;
的位置,并簡述畫圖方法;
②請說明①題中所標示![]() 點的理由.
點的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數軸上,已知在紙面上有一數軸(如圖),折疊紙面.
![]()
(1)若1表示的點與﹣1表示的點重合,則﹣2表示的點與何數表示的點重合;
(2)若﹣1表示的點與5表示的點重合,0表示的點與何數表示的點重合;
(3)若﹣1表示的點與5表示的點之間的線段折疊2次,展開后,請寫出所有的折點表示的數?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市場的公平秤如圖,把10千克的菜放到秤上,指示盤上的指針轉了180°.
(1)如果把2.75千克的菜放在秤上,指針轉過多少度?
(2)如果稱好0.5千克的菜沒有拿走,再把一捆菜放在秤上,指針共轉了![]() 那么,后放上的這捆菜有多少千克?
那么,后放上的這捆菜有多少千克?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,我們定義直線![]() 為拋物線
為拋物線![]() 、b、c為常數,
、b、c為常數,![]() 的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.
的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.

已知拋物線![]() 與其“夢想直線”交于A、B兩點
與其“夢想直線”交于A、B兩點![]() 點A在點B的左側
點A在點B的左側![]() ,與x軸負半軸交于點C.
,與x軸負半軸交于點C.
![]() 填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
填空:該拋物線的“夢想直線”的解析式為______,點A的坐標為______,點B的坐標為______;
![]() 如圖,點M為線段CB上一動點,將
如圖,點M為線段CB上一動點,將![]() 以AM所在直線為對稱軸翻折,點C的對稱點為N,若
以AM所在直線為對稱軸翻折,點C的對稱點為N,若![]() 為該拋物線的“夢想三角形”,求點N的坐標;
為該拋物線的“夢想三角形”,求點N的坐標;
![]() 當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某經銷商銷售一種產品,這種產品的成本價為10元/千克,已知銷售價不低于成本價,且物價部門規定這種產品的銷售價不高于18元/千克,市場調查發現,該產品每天的銷售量y(千克)與銷售價x(元/千克)之間的函數關系如圖所示:
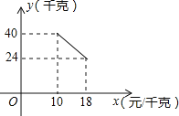
(1)求y與x之間的函數關系式,并寫出自變量x的取值范圍;
(2)求每天的銷售利潤W(元)與銷售價x(元/千克)之間的函數關系式.當銷售價為多少時,每天的銷售利潤最大?最大利潤是多少?
(3)該經銷商想要每天獲得150元的銷售利潤,銷售價應定為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:若一個三位數是312,則百位上數字為3,十位上數字為1,個位上數字為2,這個三位數可表示為3×100+1×10+2;若一個三位數是﹣312,則百位上數字為3,十位上數字為1,個位上數字為2,這個三位數可表示為﹣(3×100+1×10+2);
應用:有一個正的四位數,千位上數字為a,百位上數字為b,十位上數字為c,個位數字為d,且a>d,b﹣c>1.按順序完成一下運算;
第一步:交換千位和個位上的數字也交換百位和十位上的數字,而構成另一個四位數;
第二步:用原四位數減去第一步構成的四位數,把這個新四位數記為M;
第三步:交換M的百位和十位上的數字,又構成一個新四位數,記為N;
第四部,將M和N相加
(1)第一步構成的另一個四位數可表示為 ;
(2)試判斷M百位和十位的數字之和是否為定值?請說明理由.
(3)若M和N相加的值為8892,求a﹣d的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com