(2010•德州)為迎接第四屆世界太陽城大會,德州市把主要路段路燈更換為太陽能路燈.已知太陽能路燈售價為5000元/個,目前兩個商家有此產品.甲商家用如下方法促銷:若購買路燈不超過100個,按原價付款;若一次購買100個以上,且購買的個數每增加一個,其價格減少10元,但太陽能路燈的售價不得低于3500元/個.乙店一律按原價的80%銷售.現購買太陽能路燈x個,如果全部在甲商家購買,則所需金額為y1元;如果全部在乙商家購買,則所需金額為y2元.
(1)分別求出y1、y2與x之間的函數關系式;
(2)若市政府投資140萬元,最多能購買多少個太陽能路燈?
【答案】
分析:(1)對甲,由于購買個數不同,售價也不同,因此需按購買個數分成三段由等量關系“所需金額=售價×購買個數”列出函數關系式;
對乙,按等量關系“所需金額=售價×購買個數”列出函數關系式.
(2)分別計算投資額在甲乙商家各能購買的太陽能路燈的數量,比較得出最大值.
解答:解:(1)由題意可知,
當0<x≤100時,購買一個需5000元,故y
1=5000x;
當x>100時,
∵購買個數每增加一個,其價格減少10元,但售價不得低于3500元/個,
∴x≤

+100=250個.
即100<x≤250時,購買一個需5000-10(x-100)元,
故y
1=6000x-10x
2;
當x>250時,購買一個需3500元,
故y
1=3500x;
∴y
1=

,
y
2=5000×80%x=4000x.
(2)在甲商家,當0<x≤100時,y
1=5000x≤500000<1400000;
當100<x≤250時,y
1=6000x-10x
2=-10(x-300)
2+900000<1400000;
∴由3500x=1400000,得x=400;
在乙商家,由4000x=1400000,
得x=350個.
故選擇甲商家,最多能購買400個路燈.
點評:本題考查了分段函數關系式的列法,應從自變量的變化范圍入手,同時考查了最值的求法.

 +100=250個.
+100=250個. ,
,

 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案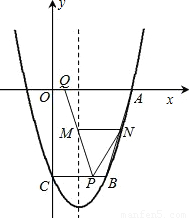
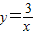 的圖象交點為A,B.
的圖象交點為A,B.