
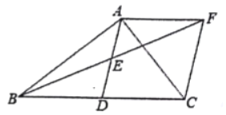
【題目】如圖,在![]() 中,
中,![]() ,AD是BC邊上的中線,點E為AD的中點,過點A作
,AD是BC邊上的中線,點E為AD的中點,過點A作![]() 交BE的延長線于點F,連接CF.
交BE的延長線于點F,連接CF.
(1)求證:![]() ;
;
(2)連接DF,當![]() 度時,四邊形ABDF為菱形?證明你的結論.
度時,四邊形ABDF為菱形?證明你的結論.
【答案】(1)見解析;(2)30
【解析】
(1)根據直角三角形的性質得到AD=CD=BD,然后證明△AEF≌△DEB即可得到結論;
(2)由條件可知四邊形ABDF是平行四邊形,然后通過30°所對的直角邊為斜邊的一半,得到AB=BD,于是得到結論.
(1)證明:∵∠BAC=90°,AD是BC邊上的中線,
∵AD=CD=BD=![]() BC,
BC,
∵點E為AD的中點,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)30°;
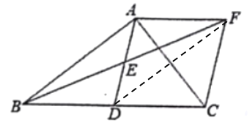
由(1)可知AF=BD,
∵AF∥BC,
∴四邊形ABDF是平行四邊形,
∵∠BAC=90°,∠ACB=30°,
∴AB=![]() BC =BD,
BC =BD,
∴平行四邊形ABDF為菱形.


科目:初中數學 來源: 題型:
【題目】某茶具店購進了A、B兩種不同的茶具,1套A種茶具和2套B種茶具共需250元;3套A種茶具和4套B種茶具共需600元.
(1)求A、B兩種茶具每套的進價分別是多少元?
(2)由于茶具暢銷,茶具店準備再購進A、B兩種茶具共80套,但這次進貨時,工廠對A種茶具每套進價提高了8%,而B種茶具每套按第一次進價的八折,若茶具店本次進貨總錢數不超過6240元,則最多可進A種茶具幾套?
(3)若銷售一套A種茶具可獲利30元,銷售一套B種茶其可獲利20元,在(2)的條件下,如何進貨可使本次購進茶具獲利最多?最多是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
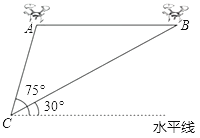
【題目】某測繪公司借助大型無人飛機航拍測繪.如圖,無人飛機從C處放飛迅速爬升到點A處,繼續水平飛行400米到達B處共需150秒,在地面C處同一方向上分別測得A處的仰角為75°,B處的仰角為30°.己知無人飛機的水平飛行速度為4米/秒,求這架無人飛機從C到A的爬升速度及水平飛行高度.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在矩形ABCD中,AB<AD,對角線AC,BD相交于點O,動點P由點A出發,沿AB-BC→CD向點D運動設點P的運動路程為x,△AOP的面積為y,y與x的函數關系圖象如圖②所小示,則AD的長為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,過
,過![]() 上到點
上到點![]() 的距離為1,3,5,7,…的點作
的距離為1,3,5,7,…的點作![]() 的垂線,分別與
的垂線,分別與![]() 相交,得到圖所示的陰影梯形,它們的面積依次記為
相交,得到圖所示的陰影梯形,它們的面積依次記為![]() ,
,![]() ,
,![]() ….則(1)
….則(1)![]() _______________;(2)通過計算可得
_______________;(2)通過計算可得![]() ______________.
______________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年疫情防控期間,我市一家服裝有限公司生產了一款服裝,為對比分析以前實體商店和現在網上商店兩種途徑的銷售情況,進行了為期30天的跟蹤調查.其中實體商店的日銷售量![]() (百件)與時間
(百件)與時間![]() (
(![]() 為整數,單位:天)的部分對應值如下表所示;網上商店的日銷售量
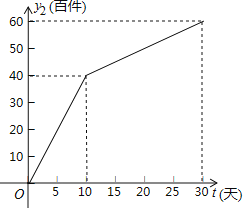
為整數,單位:天)的部分對應值如下表所示;網上商店的日銷售量![]() (百件)與時間
(百件)與時間![]() (
(![]() 為整數,單位:天)的關系如圖所示.
為整數,單位:天)的關系如圖所示.
時間 | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日銷售量 | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |
(1)請你在一次函數、二次函數和反比例函數中,選擇合適的函數反映![]() 與
與![]() 的變化規律,并求出
的變化規律,并求出![]() 與
與![]() 的函數關系式及自變量
的函數關系式及自變量![]() 的取值范圍;
的取值范圍;
(2)求![]() 與
與![]() 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)在跟蹤調查的30天中,設實體商店和網上商店的日銷售總量為![]() (百件),求
(百件),求![]() 與
與![]() 的函數關系式;當
的函數關系式;當![]() 為何值時,日銷售量
為何值時,日銷售量![]() 達到最大,并求出此時的最大值.
達到最大,并求出此時的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 年初,一場突如其來的冠狀肺炎肆虐全國,學生經歷了“停課不停學”,疫情逐漸消退.某校在開學前夕,準備買一批酒精和
年初,一場突如其來的冠狀肺炎肆虐全國,學生經歷了“停課不停學”,疫情逐漸消退.某校在開學前夕,準備買一批酒精和![]() 消毒液對校園進行消毒,經調查,若購買
消毒液對校園進行消毒,經調查,若購買![]() 箱酒精和
箱酒精和![]() 箱
箱![]() 消毒液共需
消毒液共需![]() 元,購買
元,購買![]() 箱酒精和
箱酒精和![]() 箱
箱![]() 消毒液共需
消毒液共需![]() 元.
元.
(1)求酒精和![]() 消毒液的單價;
消毒液的單價;
(2)根據學校實際情況,需從該商店一次性購買酒精和![]() 消毒液共
消毒液共![]() 箱,總費用不超過
箱,總費用不超過![]() 元,那么最多可以購買多少箱
元,那么最多可以購買多少箱![]() 消毒液?
消毒液?
(3)由于分階段開學,九年級學生第一批開學,年級組長張老師準備用![]() 元購買一批酒精和
元購買一批酒精和![]() 消毒液進行先期消毒,在錢剛好用完的條件下,他有哪幾種購買方案?
消毒液進行先期消毒,在錢剛好用完的條件下,他有哪幾種購買方案?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com