【答案】
分析:(1)此題的關鍵是求出三個待定系數,首先由“當x=-4和x=2時二次函數的函數值y相等”確定拋物線的對稱軸,進而能求出a、b間的數量關系,由C點坐標不難得出c的值,再代入A點坐標后即可得解.
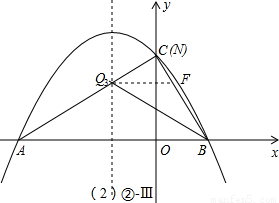
(2)①由(1)的結果不難得出B點的坐標,此時可以發現△ABC恰好是一個含30°角的特殊直角三角形,即∠ABC=60°,因此△BMN是一個等邊三角形,而四邊形BNPM是一個菱形,即BM=BN=PN=t,由于PN∥AB,根據平行線分線段成比例定理可列出關于PN、AB、CN、CB的比例關系式,根據此時可求出t的值;
在求點P的坐標時,首先要求出直線AC的解析式,點P的縱坐標可由△BNM的高得出,則P點坐標不難求出.
②在①中,已經得到了△ABC的特殊形狀,顯然△AOC的形狀和△ABC是完全一樣的,所以若以B、N、Q為頂點的三角形與△AOC相似,那么△BNQ也必須是一個含30°角的直角三角形,所以可以分兩種情況討論:
Ⅰ、∠BNQ是直角,由于∠NBM是60°,那么點Q必須在x軸上,即點Q為拋物線對稱軸與x軸的交點;
Ⅱ、∠NBQ是直角,此時BQ∥AC,即兩條直線的斜率相等,首先求出直線BQ的解析式,聯立拋物線對稱軸方程即可得到Q點的坐標.
③此題需要注意三個關鍵位置:P落在y軸上時(設此時t=α)、點M和點O重合時(設此時t=β)、P落在AC上時(設此時t=γ),那么整體上可以分四段:
Ⅰ、0<t≤α時,△PMN和△AOC不重合,S=0;
Ⅱ、α<t≤β時(參照解答部分③-Ⅱ圖),△PMN和△AOC的重合部分是個含30°角的小直角三角形,首先在Rt△BOC中由平行線分線段成比例定理求出GH的表達式,進而得出PG的長,而GH=
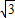
PG,則△PGH的面積(即S)可求;
Ⅲ、β<t≤γ時(參照解答部分③-Ⅲ圖),△PMN和△AOC的重合部分是個不規則圖形,其面積可由△PMN的面積(即△BMN的面積)減去含30°角的小直角三角形得出;
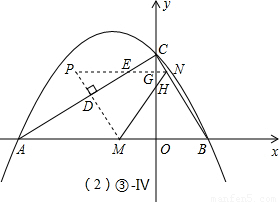
Ⅳ、γ<t≤2時(參照解答部分③-Ⅳ圖),△PMN和△AOC的重合部分是個不規則圖形,其面積可由△PMN的面積(即△BMN的面積)減去兩個含30°角的小直角三角形得出.
解答:解:(1)∵當x=-4和x=2時二次函數的函數值y相等,
∴拋物線對稱軸:x=-
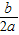
=-1,即b=2a;
由C(0,
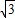
)得:c=
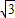
;
將A(-3,0)代入y=ax
2+2ax+
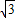
(a≠0)中,得:
9a-6a+
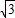
=0,a=-
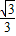
∴拋物線的解析式:y=-
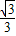
x
2-
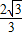
x+
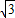
.
(2)由(1)的拋物線解析式知:A(-3,0)、B(1,0)、C(0,
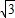
),則:
OA=3,OB=1,OC=
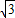
,即 OC
2=OA•OB,又OC⊥AB,則△ABC是直角三角形,且∠CAB=30°,∠ABC=60°;
①△BMN中,BM=BN=t,∠NBM=60°,即△BNM是等邊三角形;
由于△PMN由△BMNA翻轉所得,所以△PMN也是等邊三角形,四邊形PNBM是菱形;
∴PN∥AB(如題干圖),得:
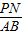
=
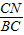
,代入數據,有:
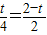
,解得:t=

;
由tan∠CAO=
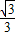
、C(0,
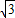
)得,直線AC:y=
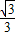
x+
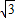
;
當y=t•sin60°=
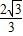
時,
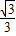
x+
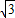
=
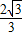
,x=-1
即 P(-1,
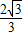
);
綜上,B點恰好落在AC邊上的P處時,t=

,P(-1,
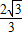
).
②∵△AOC是一個含30°角的直角三角形,
∴若以B、N、Q為頂點的三角形與△A0C相似,那么△BNQ也必須是一個含30°角的直角三角形.
分三種情況討論:
Ⅰ、∠QNB=90°、∠BQN=30°(如②-Ⅰ圖);
∵∠ABC=∠Q
1BN=60°,∴點Q
1在x軸上,即Q
1(-1,0);
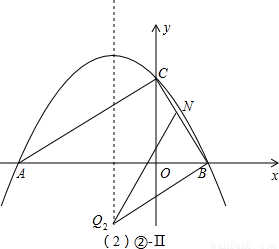
Ⅱ、∠QBN=90°、∠BQN=30°(如②-Ⅱ圖);
此時BQ
2∥AC,設直線BQ
2:y=
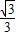
x+b,代入B(1,0),得:b=-
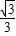
∴直線BQ
2:y=
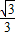
x-
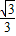
,Q
2(-1,-
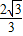
);
Ⅲ、∠QNB=90°、∠QBN=30°(如②-Ⅲ圖);
此時N、C重合,點Q
3應在①的P點處,由①的計算結果知:
Q
3C=

•sin60°=
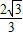
,而BC=2,即∠CQ
3B=60°,符合條件;
即 Q
3(-1,
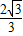
);
綜上,符合條件的Q點的坐標為:Q
1(-1,0)、Q
2(-1,-
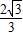
)、Q
3(-1,
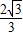
).
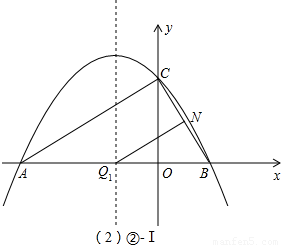
③當點P落在y軸上時,
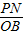
=
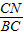
,即

=
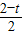
,解得:t=

;
當點M、O重合時,t=OB=1;
當點P落在AC上時,由①知,t=

;
Ⅰ、當0<t≤

時,△PMN和△AOC不重合,即S=0;
Ⅱ、當

<t≤1時(如③-Ⅱ圖),由
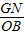
=
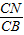
可求得:GN=1-

,PG=PN-GN=t-(1-

)=
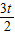
-1;
S=S
△PGH=

×(
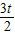
-1)×(
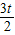
-1)
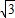
=
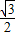
(
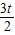
-1)
2;
Ⅲ、當1<t≤

時(如③-Ⅲ圖);
由Ⅱ知,GN=1-

,GH=
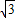
GN=
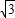
(1-

),S
△GHN=

×(1-

)×
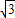
(1-

)=
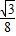
t
2-
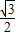
t+
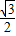
;
S=S
△PMN-S
△GHN=S
△BMN-S
△GHN=

×t×
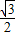
t-(
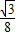
t
2-
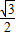
t+
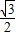
)=
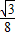
t
2+
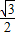
t-
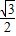
;
Ⅳ、當

<t≤2時(如③-Ⅳ圖);
同上,可求得S
△PDE=
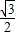
(

t-2)
2=
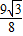
t
2-3
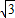
t+2
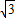
、S
△GHN=
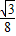
t
2-
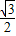
t+
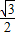
、S
△PMN=
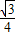
t
2,
S=S
△PMN-S
△PDE-S
△GHN=-
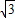
t
2+
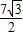
t-
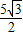
;
綜上,S=
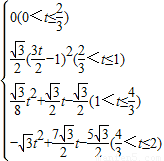
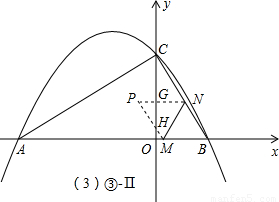
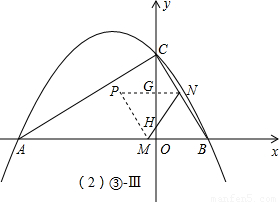
 點評:
點評:此題主要考查了二次函數解析式的確定、相似三角形的判定和性質以及圖形面積的求法;后面兩個小題的難度很大,倒數第二道題中,由于涉及到不同的相似情況,是容易漏解的地方;最后一題中,P點的不同位置確定了重合部分的形狀,一定要將所有可能的情況畫出來,然后根據圖形間的面積和差關系來進行解題.

 ),且當x=-4和x=2時二次函數的函數值y相等.
),且當x=-4和x=2時二次函數的函數值y相等.
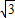 PG,則△PGH的面積(即S)可求;
PG,則△PGH的面積(即S)可求;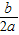 =-1,即b=2a;
=-1,即b=2a;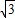 )得:c=
)得:c=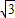 ;
;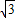 (a≠0)中,得:
(a≠0)中,得: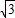 =0,a=-
=0,a=-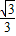
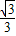 x2-
x2-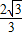 x+
x+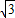 .
.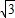 ),則:
),則: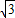 ,即 OC2=OA•OB,又OC⊥AB,則△ABC是直角三角形,且∠CAB=30°,∠ABC=60°;
,即 OC2=OA•OB,又OC⊥AB,則△ABC是直角三角形,且∠CAB=30°,∠ABC=60°;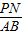 =
=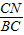 ,代入數據,有:
,代入數據,有: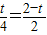 ,解得:t=
,解得:t= ;
;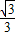 、C(0,
、C(0,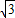 )得,直線AC:y=
)得,直線AC:y=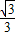 x+
x+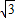 ;
;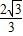 時,
時,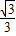 x+
x+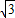 =
=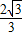 ,x=-1
,x=-1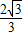 );
); ,P(-1,
,P(-1,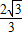 ).
).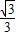 x+b,代入B(1,0),得:b=-
x+b,代入B(1,0),得:b=-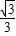
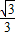 x-
x-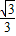 ,Q2(-1,-
,Q2(-1,-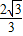 );
); •sin60°=
•sin60°=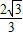 ,而BC=2,即∠CQ3B=60°,符合條件;
,而BC=2,即∠CQ3B=60°,符合條件;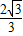 );
);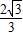 )、Q3(-1,
)、Q3(-1,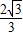 ).
).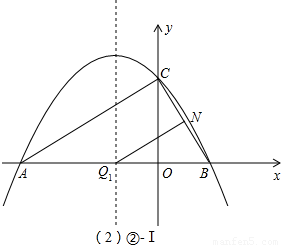


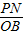 =
=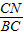 ,即
,即 =
=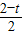 ,解得:t=
,解得:t= ;
; ;
; 時,△PMN和△AOC不重合,即S=0;
時,△PMN和△AOC不重合,即S=0; <t≤1時(如③-Ⅱ圖),由
<t≤1時(如③-Ⅱ圖),由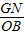 =
=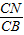 可求得:GN=1-
可求得:GN=1- ,PG=PN-GN=t-(1-
,PG=PN-GN=t-(1- )=
)=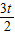 -1;
-1; ×(
×(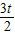 -1)×(
-1)×(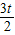 -1)
-1)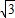 =
=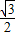 (
(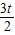 -1)2;
-1)2; 時(如③-Ⅲ圖);
時(如③-Ⅲ圖); ,GH=
,GH=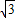 GN=
GN=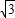 (1-
(1- ),S△GHN=
),S△GHN= ×(1-
×(1- )×
)×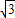 (1-
(1- )=
)=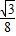 t2-
t2-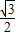 t+
t+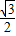 ;
; ×t×
×t×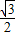 t-(
t-(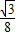 t2-
t2-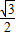 t+
t+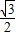 )=
)=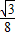 t2+
t2+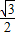 t-
t-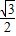 ;
; <t≤2時(如③-Ⅳ圖);
<t≤2時(如③-Ⅳ圖);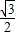 (
( t-2)2=
t-2)2=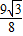 t2-3
t2-3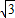 t+2
t+2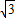 、S△GHN=
、S△GHN=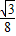 t2-
t2-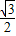 t+
t+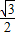 、S△PMN=
、S△PMN=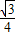 t2,
t2,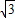 t2+
t2+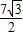 t-
t-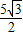 ;
;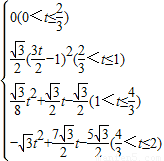
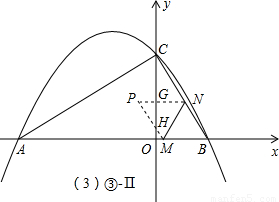
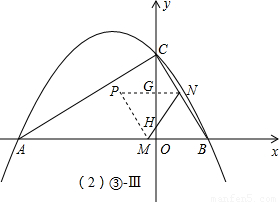



 如圖,二次函數的圖象經過點D(0,
如圖,二次函數的圖象經過點D(0,
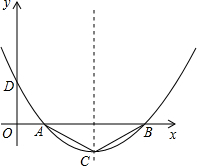
 如圖,二次函數y=ax2+bx+c的圖象與x軸交于B、C兩點,與y軸交于點A(0,-3),∠ABC=45°,∠ACB=60°,求這個二次函數解析式.
如圖,二次函數y=ax2+bx+c的圖象與x軸交于B、C兩點,與y軸交于點A(0,-3),∠ABC=45°,∠ACB=60°,求這個二次函數解析式. 某公司推出了一種高效環保型洗滌用品,年初上市后,公司經歷了從虧損到盈利的過程,如圖的二次函數圖象(部分)刻畫了該公司年初以來累積利潤s(萬元)與時間t(月)之間的關系(即前t個月的利潤總和s與t之間的關系).根據圖象提供的信息,解答下列問題:
某公司推出了一種高效環保型洗滌用品,年初上市后,公司經歷了從虧損到盈利的過程,如圖的二次函數圖象(部分)刻畫了該公司年初以來累積利潤s(萬元)與時間t(月)之間的關系(即前t個月的利潤總和s與t之間的關系).根據圖象提供的信息,解答下列問題: 如圖,二次函數y=ax2+bx+c的圖象與x軸相交于兩個點,根據圖象回答:(1)b
如圖,二次函數y=ax2+bx+c的圖象與x軸相交于兩個點,根據圖象回答:(1)b