【題目】如圖，
中，
，D是BC邊的中點，連接AD，過點A作AE∥BC，且AE＝CD，連接EC．
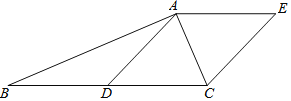
（1）求證：四邊形ADCE是菱形；
（2）如果
，
，寫出求菱形ADCE的面積的思路．
【答案】（1）詳見解析；（2）詳見解析．
【解析】
（1）先證明四邊形ADCE是平行四邊形，再由直角三角形斜邊上的中線性質得出AD＝CD，即可得出結論；
（2）由中線的性質得出△ABC的面積＝2△ACD的面積，由菱形的性質得出菱形ADCE的面積＝2△ACD的面積，得出菱形ADCE的面積＝△ABC的面積，由三角函數得出AB＝3a，即可求出答案．
（1）∵AE∥BC，AE＝CD，
∴四邊形ADCE是平行四邊形．
∵∠BAC＝90°，D是BC邊的中點，
∴AD＝BD＝CD．
∴平行四邊形ADCE是菱形．
（2）∵D是BC邊的中點，
∴△ABC的面積＝2△ACD的面積，
∵四邊形ADCE是菱形，
∴菱形ADCE的面積＝2△ACD的面積，
∴菱形ADCE的面積＝△ABC的面積，
∵∠BAC＝90°，
，
，
∴AB＝3AC＝3a，
∴菱形ADCE的面積
．
同步輕松練習系列答案
課課通課程標準思維方法與能力訓練系列答案科目：初中數學 來源： 題型：
【題目】某班數學活動小組測量吉林市“世紀之舟”的高度．他們制定了測量方案，并利用課余時間完成了實地測景，測量項目及數據如下表：
項目 | 內容 | |||
課題 | 測量吉林市“實際之舟”的高度 | |||
示意圖 |
| 如圖，用測角儀在 | ||
測量數據 |
|
|
| 測角儀 |
|
| 50米 | 1.5米 | |
… | … | |||
請你根據活動小組測得的數據，求世紀之舟的高
（結果保留小數點后一位）．
（參考數據：
，
，
）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某果品超市經銷一種水果，已知該水果的進價為每千克15元，通過一段時間的銷售情況發現，該種水果每周的銷售總額相同，且每周的銷售量y（千克）與每千克售價x（元）的關系如表所示
每千克售價x（元） | 25 | 30 | 40 |
每周銷售量y（千克） | 240 | 200 | 150 |
（1）寫出每周銷售量y（千克）與每千克售價x（元）的函數關系式；
（2）由于銷售淡季即將來臨，超市要完成每周銷售量不低于300千克的任務，則該種水果每千克售價最多定為多少元？
（3）在（2）的基礎上，超市銷售該種水果能否到達每周獲利1200元？說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司在抗震救災期間承擔40 000頂救災帳篷的生產任務，分為A、B、C、D四種型號，它們的數量百分比和每天單獨生產各種型號帳篷的數量如圖所示：
根據以上信息，下列判斷錯誤的是（ ）
A. 其中的D型帳篷占帳篷總數的10%
B. 單獨生產B型帳篷的天數是單獨生產C型帳篷天數的3倍
C. 單獨生產A型帳篷與單獨生產D型帳篷的天數相等
D. 單獨生產B型帳篷的天數是單獨生產A型帳篷天數的2倍
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某“數學興趣小組”根據學習函數的經驗，對函數
的圖象和性質進行了探究，探究過程如下，請補充完整：
(1)該函數的自變量
的取值范圍是______；
(2)同學們先找到
與的幾組對應值，然后在下圖的平面直角坐標系
中，描出各對對應值為坐標的點．請你根據描出的點，畫出該函數的圖象；
(3)結合畫出的函數圖象，寫出該函數的一條性質：_______________．
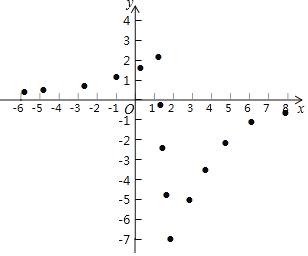
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，AC＝BC，點D是AC延長線上一點，連結BD．將
繞著點C順時針旋轉90°得到
，延長AE交BD于F．
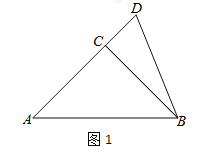
（1）依據題意補全圖1；
（2）判斷AE與BD的位置關系，說明理由；
（3）連結CF，求
的度數．
要想求出的度數，小明經過思考，得到了以下幾種想法：
想法1：在AF上取一點G，使得AG＝BF，需要先證明
，然后再證明
是等腰直角三角形．
想法2：取AB的中點O，連接OC，OF，只需要利用圓的性質證明
．
想法3：將
繞點C逆時針旋轉90°，得到
，只需證明
是等腰直角三角形．
請你參考上面的想法，幫助小明求解．（寫出一種方法即可）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，AB=BC，∠ABC=90°．以AB為斜邊作等腰直角三角形ADB．點P是直線DB上一個動點，連接AP，作PE⊥AP交BC所在的直線于點E．
（1）如圖1，點P在BD的延長線上，PE⊥EC，AD=1，直接寫出PE的長；
（2）點P在線段BD上（不與B，D重合），依題意，將圖2補全，求證：PA=PE；
（3）點P在DB的延長線上，依題意，將圖3補全，并判斷PA=PE是否仍然成立．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中拋物線y＝﹣x2+bx+c經過點A、B、C，已知A（﹣1，0），C（0，3）．
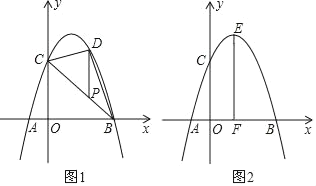
（1）求拋物線的表達式；
（2）如圖1，P為線段BC上一點，過點P作y軸平行線，交拋物線于點D，當△BCD的面積最大時，求點P的坐標；
（3）如圖2，拋物線頂點為E，EF⊥x軸于F點，N是線段EF上一動點，M（m，0）是x軸上一動點，若∠MNC＝90°，直接寫出實數m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
