
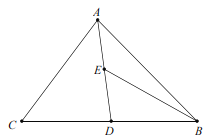
【題目】如圖,![]() 中,
中,![]() 為
為![]() 上一點,連接
上一點,連接![]() ,
,![]() ,點
,點![]() 在
在![]() 上,連接BE,∠C=∠DEB,若BE=3,AB=4,則線段AE的長為_____.
上,連接BE,∠C=∠DEB,若BE=3,AB=4,則線段AE的長為_____.
科目:初中數學 來源: 題型:
【題目】如圖所示,請按照要求解答問題.
(1)數軸上的點C在2、3的正中間位置,則點C表示的數是 ,線段AB的中點D表示的數是 ;
(2)線段AB的中點D與線段BC的中點E的距離為 ;
(3)在數軸上方有一點M,下方有一點N,且∠ABM=120°,∠CBN=60°,請畫出示意圖,并判斷BC是否平分∠MBN.簡要說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(探究活動)
(1)問題發現:如圖①,直線AB∥CD,E是AB與AD之間的一點,連接BE,CE,可以發現∠B+∠C=∠BEC.

請把下面的證明過程補充完整:
證明:過點E作EF∥AB,
∵AB∥DC(已知),EF∥AB(輔助線的作法),
∴EF∥DC( )
∴∠C=∠CEF.( )
∵EF∥AB,∴∠B=∠BEF(同理),
∴∠B+∠C= (等量代換)
即∠B+∠C=∠BEC.
(2)拓展探究:如果點E運動到圖②所示的位置,其他條件不變,試探究∠B、∠C、∠BEC的數量關系并證明;
(3)解決問題:如圖③,AB∥DC,∠C=120°,∠AEC=80°,則∠A= .(直接寫出結論,不用寫計算過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系xOy中,對于點P(a,b),若點P′的坐標為(a ![]() ,ka+b)(其中k為常數,且k≠0),則稱點P′為點P的“k關聯點”.
,ka+b)(其中k為常數,且k≠0),則稱點P′為點P的“k關聯點”.
(1)求點P(﹣2,3)的“2關聯點”P′的坐標;
(2)若a、b為正整數,點P的“k關聯點”P′的坐標為(3,6),求出k及點P的坐標;
(3)如圖,點Q的坐標為(0,4 ![]() ),點A在函數y=﹣
),點A在函數y=﹣ ![]() (x<0)的圖象上運動,且點A是點B的“﹣
(x<0)的圖象上運動,且點A是點B的“﹣ ![]() 關聯點”,當線段BQ最短時,求B點坐標.
關聯點”,當線段BQ最短時,求B點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】霧霾天氣嚴重影響市民的生活質量.在去年寒假期間,某校八年級一班的綜合實踐小組同學對“霧霾天氣的主要成因”隨機調查了所在城市部分市民.并對調查結果進行了整理.繪制了如圖不完整的統計圖表.觀察分析并回答下列問題.
組別 | 霧霾天氣的主要成因 | 百分比 |
A | 工業污染 | 45% |
B | 汽車尾氣排放 | m |
C | 爐煙氣排放 | 15% |
D | 其他(濫砍濫伐等) | n |
(1)本次被調查的市民共有多少人?
(2)求m、n的值,并計算圖2中區域B所對應的扇形圓心角的度數;
(3)若該市有100萬人口,請估計持有A、B兩組主要成因的市民有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,BC=6,D為AC延長線上一點,AC=3CD,過點D作DH∥AB,交BC的延長線于點H.
(1)求BH的長;
(2)若AB=12,試判斷∠CBD與∠A的數量關系,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知射線AB∥射線CD,P為一動點,AE平分∠PAB,CE平分∠PCD,且AE與CE相交于點E.

(1)在圖1中,當點P運動到線段AC上時,∠APC=180°.
①直接寫出∠AEC的度數;②求證:∠AEC=∠EAB+∠ECD;
(2)當點P運動到圖2的位置時,猜想∠AEC與∠APC之間的關系,并加以說明;
(3)當點P運動到圖3的位置時,(2)中的結論是否還成立?若成立,請說明理由;若不成立,請寫出∠AEC與∠APC之間的關系,并加以證明。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的面積為8cm2 , AP垂直∠B的平分線BP于P,則△PBC的面積為( )

A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com