
 >0>x1),與y軸交于C點,且∠BAC=∠BCO.
>0>x1),與y軸交于C點,且∠BAC=∠BCO. ,0)為圓心作⊙D,與y軸相切于點O.過拋物線上一點E(x3,t)(t>0,x3<0)作x軸的平行線與⊙D交于F、G兩點,與拋物線交于另一點H.問:是否存在實數t,使得EF+GH=FG?如果存在,求出t的值;如果不存在,請說明理由.
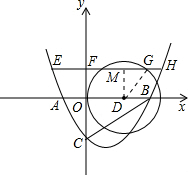
,0)為圓心作⊙D,與y軸相切于點O.過拋物線上一點E(x3,t)(t>0,x3<0)作x軸的平行線與⊙D交于F、G兩點,與拋物線交于另一點H.問:是否存在實數t,使得EF+GH=FG?如果存在,求出t的值;如果不存在,請說明理由. ,
,

 =2
=2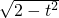 ,
,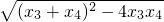 =
=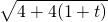 =2
=2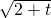 ,
,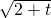 =4
=4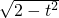 ,
,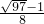 ,t2=-
,t2=-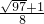 (舍去),
(舍去),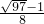 ,使得EF+GH=FG.
,使得EF+GH=FG.

科目:初中數學 來源: 題型:
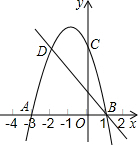 次函數的圖象上,且D與C關于對稱軸對稱,一次函數的圖象過點B、D;
次函數的圖象上,且D與C關于對稱軸對稱,一次函數的圖象過點B、D;查看答案和解析>>
科目:初中數學 來源: 題型:
 已知關于x的二次函數y=x2+(2k-1)x+k2-1.
已知關于x的二次函數y=x2+(2k-1)x+k2-1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知關于x的二次函數y=x2+(2k-1)x+k2-1.
已知關于x的二次函數y=x2+(2k-1)x+k2-1.查看答案和解析>>
科目:初中數學 來源:2011年廣東省廣州市白云區中考數學一模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com