
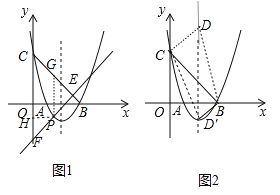
【題目】如圖,拋物線![]() 與x軸交于A,B兩點,B點坐標為(3,0).與y軸交于點C(0,3).
與x軸交于A,B兩點,B點坐標為(3,0).與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)點P在x軸下方的拋物線上,過點P的直線y=x+m與直線BC交于點E,與y軸交于點F,求PE+EF的最大值;
(3)點D為拋物線對稱軸上一點.
①當△BCD是以BC為直角邊的直角三角形時,求點D的坐標;
②若△BCD是銳角三角形,求點D的縱坐標的取值范圍.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)①D點坐標為(2,5)或(2,﹣1);②點D的縱坐標的取值范圍為
;(3)①D點坐標為(2,5)或(2,﹣1);②點D的縱坐標的取值范圍為![]() <y<5或﹣1<y<
<y<5或﹣1<y<![]() .
.
【解析】試題分析:(1)利用待定系數法求拋物線的解析式;
(2)易得BC的解析式為y=﹣x+3,先證明△ECF為等腰直角三角形,作PH⊥y軸于H,PG∥y軸交BC于G,如圖1,則△EPG為等腰直角三角形,PE=![]() PG,設P(t,t2﹣4t+3)(1<t<3),則G(t,﹣t+3),接著利用t表示PF、PE,所以PE+EF=2PE+PF=
PG,設P(t,t2﹣4t+3)(1<t<3),則G(t,﹣t+3),接著利用t表示PF、PE,所以PE+EF=2PE+PF= ![]() ,然后利用二次函數的性質解決問題;
,然后利用二次函數的性質解決問題;
(3)①如圖2,拋物線的對稱軸為直線x=2,設D(2,y),利用兩點間的距離公式得到BC2=18,DC2=4+(y﹣3)2,BD2=1+y2,討論:當△BCD是以BC為直角邊,BD為斜邊的直角三角形時,18+4+(y﹣3)2=1+y2;當△BCD是以BC為直角邊,CD為斜邊的直角三角形時,4+(y﹣3)2=1+y2+18,分別解方程求出t即可得到對應的D點坐標;
②由于△BCD是以BC為斜邊的直角三角形有4+(y﹣3)2+1+y2=18,解出y的值,得到此時D點的坐標,然后結合圖形可確定△BCD是銳角三角形時點D的縱坐標的取值范圍.
試題解析:解:(1)把B(3,0),C(0,3)代入![]() 得:
得: ![]() ,解得:
,解得: ![]() ,∴拋物線的解析式為
,∴拋物線的解析式為![]() ;
;
(2)易得BC的解析式為y=﹣x+3,∵直線y=x﹣m與直線y=x平行,∴直線y=﹣x+3與直線y=x﹣m垂直,∴∠CEF=90°,∴△ECF為等腰直角三角形,作PH⊥y軸于H,PG∥y軸交BC于G,如圖1,△EPG為等腰直角三角形,PE=![]() PG,設P(t,t2﹣4t+3)(1<t<3),則G(t,﹣t+3),∴PF=
PG,設P(t,t2﹣4t+3)(1<t<3),則G(t,﹣t+3),∴PF=![]() PH=
PH=![]() t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=
t,PG=﹣t+3﹣(t2﹣4t+3)=﹣t2+3t,∴PE=![]() PG=
PG= ![]() ,∴PE+EF=PE+PE+PF=2PE+PF=
,∴PE+EF=PE+PE+PF=2PE+PF= ![]() =
= ![]() =
=![]() ,當t=2時,PE+EF的最大值為
,當t=2時,PE+EF的最大值為![]() ;
;
(3)①如圖2,拋物線的對稱軸為直線x=![]() =2,設D(2,y),則BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,當△BCD是以BC為直角邊,BD為斜邊的直角三角形時,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得y=5,此時D點坐標為(2,5);
=2,設D(2,y),則BC2=32+32=18,DC2=4+(y﹣3)2,BD2=(3﹣2)2+y2=1+y2,當△BCD是以BC為直角邊,BD為斜邊的直角三角形時,BC2+DC2=BD2,即18+4+(y﹣3)2=1+y2,解得y=5,此時D點坐標為(2,5);
當△BCD是以BC為直角邊,CD為斜邊的直角三角形時,BC2+DB2=DC2,即4+(y﹣3)2=1+y2+18,解得y=﹣1,此時D點坐標為(2,﹣1);
綜上所述:D點坐標為(2,5)或(2,﹣1).
②當△BCD是以BC為斜邊的直角三角形時,DC2+DB2=BC2,即4+(y﹣3)2+1+y2=18,解得y1=![]() ,y2=
,y2=![]() ,此時D點坐標為(2,
,此時D點坐標為(2, ![]() )或(2,
)或(2, ![]() ),所以△BCD是銳角三角形,點D的縱坐標的取值范圍為
),所以△BCD是銳角三角形,點D的縱坐標的取值范圍為![]() <y<5或﹣1<y<
<y<5或﹣1<y<![]() .
.


科目:初中數學 來源: 題型:
【題目】某玩具廠有4個車間,某周是質量檢查周,現每個車間都原有a(a>0)個成品,且每個車間每天都生產b(b>0)個成品,質量科派出若干名檢驗員周一、周二檢驗其中兩個車間原有的和這兩天生產的所有成品,然后,周三到周五檢驗另外兩個車間原有的和本周生產的所有成品,假定每名檢驗員每天檢驗的成品數相同.
(1)這若干名檢驗員1天共檢驗多少個成品?(用含a、b的代數式表示)
(2)若一名檢驗員1天能檢驗![]() b個成品,則質量科至少要派出多少名檢驗員?
b個成品,則質量科至少要派出多少名檢驗員?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】攀枝花芒果由于品質高、口感好而聞名全國,通過優質快捷的網絡銷售渠道,小明的媽媽先購買了2箱A品種芒果和3箱B品種芒果,共花費450元;后又購買了l箱A品種芒果和2箱B品種芒果,共花費275元(每次兩種芒果的售價都不變).
(1)問A品種芒果和B品種芒果的售價分別是每箱多少元?
(2)現要購買兩種芒果共18箱,要求B品種芒果的數量不少于A品種芒果數量的2倍,但不超過A品種芒果數量的4倍,請你設計購買方案,并寫出所需費用最低的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據官方數據統計,70周年國慶閱兵網上總觀看人次突破513000000,最高同時在線人數突破600萬.將513000000用科學記數法表示應為( )
A.5.13×108B.5.13×109C.513×106D.0.513×109
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com