
【題目】如圖,直線y=﹣x﹣4與拋物線y=ax2+bx+c相交于A,B兩點,其中A,B兩點的橫坐標分別為﹣1和﹣4,且拋物線過原點.
(1)求拋物線的解析式;
(2)在坐標軸上是否存在點C,使△ABC為等腰三角形?若存在,求出點C的坐標,若不存在,請說明理由;
(3)若點P是線段AB上不與A,B重合的動點,過點P作PE∥OA,與拋物線第三象限的部分交于一點E,過點E作EG⊥x軸于點G,交AB于點F,若S△BGF=3S△EFP , 求 ![]() 的值.
的值.
【答案】
(1)
解:∵A,B兩點在直線y=﹣x﹣4上,且橫坐標分別為﹣1、﹣4,
∴A(﹣1,﹣3),B(﹣4,0),
∵拋物線過原點,
∴c=0,
把A、B兩點坐標代入拋物線解析式可得 ![]() ,解得
,解得 ![]() ,
,
∴拋物線解析式為y=x2+4x
(2)
解:∵△ABC為等腰三角形,
∴有AB=AC、AB=BC和CA=CB三種情況,
①當AB=AC時,當點C在y軸上,設C(0,y),
則AB= ![]() =3
=3 ![]() ,AC=
,AC= ![]() ,
,
∴3 ![]() =
= ![]() ,解得y=﹣3﹣
,解得y=﹣3﹣ ![]() 或y=﹣3+
或y=﹣3+ ![]() ,
,
∴C(0,﹣3﹣ ![]() )或(0,﹣3﹣
)或(0,﹣3﹣ ![]() );
);
當點C在x軸上時,設C(x,0),則AC= ![]() ,
,
∴ ![]() =3
=3 ![]() ,解得x=﹣4或x=2,當x=﹣4時,B、C重合,舍去,
,解得x=﹣4或x=2,當x=﹣4時,B、C重合,舍去,
∴C(2,0);
②當AB=BC時,當點C在x軸上,設C(x,0),
則有AB=3 ![]() ,BC=|x+4|,
,BC=|x+4|,
∴|x+4|=3 ![]() ,解得x=﹣4+3
,解得x=﹣4+3 ![]() 或x=﹣4﹣3
或x=﹣4﹣3 ![]() ,
,
∴C(﹣4+3 ![]() ,0)或(﹣4﹣3
,0)或(﹣4﹣3 ![]() ,0);
,0);
當點C在y軸上,設C(0,y),則BC= ![]() ,
,
∴ ![]() =3
=3 ![]() ,解得y=
,解得y= ![]() 或y=﹣
或y=﹣ ![]() ,
,
∴C(0, ![]() )或(0,﹣
)或(0,﹣ ![]() );
);
③當CB=CA時,則點C在線段AB的垂直平分線與y軸的交點處,
∵A(﹣1,﹣3),B(﹣4,0),
∴線段AB的中點坐標為(﹣ ![]() ,﹣
,﹣ ![]() ),
),
設線段AB的垂直平分線的解析式為y=x+d,
∴﹣ ![]() =﹣
=﹣ ![]() +d,解得d=1,
+d,解得d=1,
∴線段AB的垂直平分線的解析式為y=x+1,
令x=0可得y=1,令y=0可求得x=﹣1,
∴C(﹣1,0)或(0,1);
綜上可知存在滿足條件的點C,其坐標為(0,﹣3﹣ ![]() )或(0,﹣3﹣
)或(0,﹣3﹣ ![]() )或(﹣4+3
)或(﹣4+3 ![]() ,0)或(﹣4﹣3
,0)或(﹣4﹣3 ![]() ,0)或(﹣1,0)或(0,1)或(2,0)或(0,
,0)或(﹣1,0)或(0,1)或(2,0)或(0, ![]() )或(0,﹣
)或(0,﹣ ![]() )
)
(3)
解:過點P作PQ⊥EF,交EF于點Q,過點A作AD⊥x軸于點D,
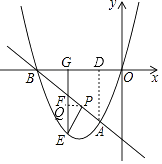
∵PE∥OA,GE∥AD,
∴∠OAD=∠PEG,∠PQE=∠ODA=90°,
∴△PQE∽△ODA,
∴ ![]() =3,即EQ=3PQ,
=3,即EQ=3PQ,
∵直線AB的解析式為y=﹣x﹣4,
∴∠ABO=45°=∠PFQ,
∴PQ=FQ,BG=GF,
∴EF=4PQ,
∴GE=GF+4PQ,
∵S△BGF=3S△EFP,
∴ ![]() GF2=3×
GF2=3× ![]() 4PQ2,
4PQ2,
∴GF=2 ![]() PQ,
PQ,
∴ ![]() =
= ![]() =
= ![]()
【解析】(1)由直線解析式可分別求得A、B兩點的坐標,利用待定系數法可求得拋物線解析式;(2)當AB=AC時,點C在y軸上,可表示出AC的長度,可求得其坐標;當AB=BC時,可知點C在x軸上,可表示出BC的長度,可求得其坐標;當AC=BC時點C在線段AB的垂直平分線與坐標軸的交點處,可求得線段AB的中點的坐標,可求得垂直平分線的解析式,則可求得C點坐標;(3)過點P作PQ⊥EF,交EF于點Q,過點A作AD⊥x軸于點D,可證明△PQE∽△ODA,可求得EQ=3PQ,再結合F點在直線AB上,可求得FQ=PQ,則可求得EF=4PQ,利用三角形的面積的關系可求得GF與PQ的關系,則可求得比值.


科目:初中數學 來源: 題型:
【題目】折疊三角形紙片ABC,使點A落在BC邊上的點F,且折痕DE∥BC,若∠A=75°,∠C=60°,則∠BDF=____________________________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,BC=5 ![]() ,∠C=30°.點D從點C出發沿CA方向以每秒2個單位長的速度向點A勻速運動,同時點E從點A出發沿AB方向以每秒1個單位長的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t秒(t>0).過點D作DF⊥BC于點F,連接DE、EF.
,∠C=30°.點D從點C出發沿CA方向以每秒2個單位長的速度向點A勻速運動,同時點E從點A出發沿AB方向以每秒1個單位長的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t秒(t>0).過點D作DF⊥BC于點F,連接DE、EF. 
(1)求證:AE=DF;
(2)四邊形AEFD能夠成為菱形嗎?如果能,求出相應的t值;如果不能,說明理由.
(3)當t為何值時,△DEF為直角三角形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線AB,CD相交于點O,OE平分∠AOD,FO⊥AB,垂足為O,![]() ∠BOD=∠DOE.
∠BOD=∠DOE.
(1)求∠BOF的度數;
(2)請寫出圖中與∠BOD相等的所有的角.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面內,分別用3根、5根、6根……火柴棒首尾依次相接,能搭成什么形狀的三角形呢?通過嘗試,列表如下.
火柴棒數 | 3 | 5 | 6 | … |
示意圖 |
|
|
| … |
形狀 | 等邊三角形 | 等腰三角形 | 等邊三角形 | … |
問:(1)4根火柴棒能搭成三角形嗎?
(2)8根、12根火柴棒分別能搭成幾種不同形狀的三角形?并畫出它們的示意圖.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在扇形OAB中,∠O=60°,OA=4 ![]() ,四邊形OECF是扇形OAB中最大的菱形,其中點E,C,F分別在OA,
,四邊形OECF是扇形OAB中最大的菱形,其中點E,C,F分別在OA, ![]() ,OB上,則圖中陰影部分的面積為 .
,OB上,則圖中陰影部分的面積為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有正方形ABCD和一個以O為直角頂點的三角板,移動三角板,使三角板的兩直角邊所在直線分別與直線BC,CD交于點M,N.
(1)如圖1,若點O與點A重合,則OM與ON的數量關系是__________________;
(2)如圖2,若點O在正方形的中心(即兩對角線的交點),則(1)中的結論是否仍然成立?請說明理由;
(3)如圖3,若點O在正方形的內部(含邊界),當OM=ON時,請探究點O在移動過程中可形成什么圖形?
(4)如圖4是點O在正方形外部的一種情況.當OM=ON時,請你就“點O的位置在各種情況下(含外部)移動所形成的圖形”提出一個正確的結論.(不必說理)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com