
 =
= ,
, =
=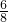 ,
, =
=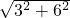 =3
=3 ,
, =
=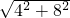 =4
=4 ,
,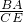 =
=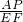
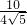 =
=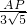 ,
,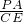 =
= ,
,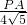 =
=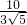 ,
, ,
, ).
).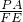 =
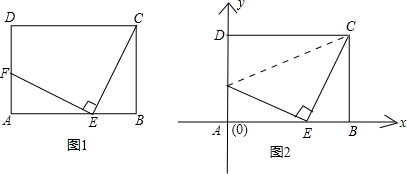
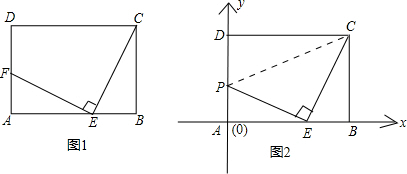
=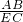 ,則△EFA∽△CEB;由勾股定理可求出FE和EC,根據相似可求出點P的坐標.
,則△EFA∽△CEB;由勾股定理可求出FE和EC,根據相似可求出點P的坐標.

科目:初中數學 來源: 題型:
 如圖,在矩形ABCD中,連接AC,如果O為△ABC的內心,過O作OE⊥AD于E,作OF⊥CD于F,則矩形OFDE的面積與矩形ABCD的面積的比值為( )
如圖,在矩形ABCD中,連接AC,如果O為△ABC的內心,過O作OE⊥AD于E,作OF⊥CD于F,則矩形OFDE的面積與矩形ABCD的面積的比值為( )A、
| ||
B、
| ||
C、
| ||
| D、不能確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 Q兩點相遇時,它們同時停止運動.設P、Q兩點運動的時間為x(秒),△APQ的面積為S(平方單位).
Q兩點相遇時,它們同時停止運動.設P、Q兩點運動的時間為x(秒),△APQ的面積為S(平方單位).| 7 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•南京)如圖,將矩形ABCD繞點A順時針旋轉到矩形AB′C′D′的位置,旋轉角為α(0°<α<90°),若∠1=110°,則∠α=
(2013•南京)如圖,將矩形ABCD繞點A順時針旋轉到矩形AB′C′D′的位置,旋轉角為α(0°<α<90°),若∠1=110°,則∠α=查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com