
【題目】問題原型:如圖①,在等腰直角三角形ABC中,∠ACB=90°,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.過點D作△BCD的BC邊上的高DE,
易證△ABC≌△BDE,從而得到△BCD的面積為 ![]() .
.
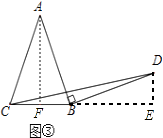
初步探究:如圖②,在Rt△ABC中,∠ACB=90°,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.用含a的代數式表示△BCD的面積,并說明理由.
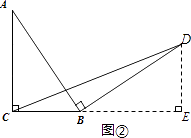
簡單應用:如圖③,在等腰三角形ABC中,AB=AC,BC=a.將邊AB繞點B順時針旋轉90°得到線段BD,連結CD.直接寫出△BCD的面積.(用含a的代數式表示)
【答案】解:初步探究:△BCD的面積為 ![]() .
.
理由:如圖②,過點D作BC的垂線,與BC的延長線交于點E.
∴∠BED=∠ACB=90°.
∵線段AB繞點B順時針旋轉90°得到線段BE,
∴AB=BD,∠ABD=90°.
∴∠ABC+∠DBE=90°.
∵∠A+∠ABC=90°.
∴∠A=∠DBE.
在△ABC和△BDE中, ,
,
∴△ABC≌△BDE(AAS)
∴BC=DE=a.
∵S△BCD= ![]() BCDE
BCDE
∴S△BCD= ![]() ;
;
簡單應用:如圖③,過點A作AF⊥BC與F,過點D作DE⊥BC的延長線于點E,
∴∠AFB=∠E=90°,BF= ![]() BC=
BC= ![]() a.
a.
∴∠FAB+∠ABF=90°.
∵∠ABD=90°,
∴∠ABF+∠DBE=90°,
∴∠FAB=∠EBD.
∵線段BD是由線段AB旋轉得到的,
∴AB=BD.
在△AFB和△BED中,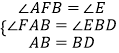 ,
,
∴△AFB≌△BED(AAS),
∴BF=DE= ![]() a.
a.
∵S△BCD= ![]() BCDE,
BCDE,
∴S△BCD= ![]()
![]() aa=
aa= ![]() a2 .
a2 .
∴△BCD的面積為 ![]() .
.
【解析】初步探究:如圖②,過點D作BC的垂線,與BC的延長線交于點E,由垂直的性質就可以得出△ABC≌△BDE,就有DE=BC=a.進而由三角形的面積公式得出結論;
簡單運用:如圖③,過點A作AF⊥BC與F,過點D作DE⊥BC的延長線于點E,由等腰三角形的性質可以得出BF= ![]() BC,由條件可以得出△AFB≌△BED就可以得出BF=DE,由三角形的面積公式就可以得出結論.
BC,由條件可以得出△AFB≌△BED就可以得出BF=DE,由三角形的面積公式就可以得出結論.


科目:初中數學 來源: 題型:
【題目】如圖,點F,G分別在△ADE的AD,DE邊上,C,B依次為GF延長線上兩點,AB=AD,∠BAF=∠CAE,∠B=∠D.
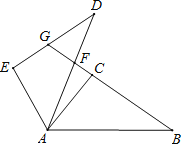
(1)求證:BC=DE;
(2)若∠B=35°,∠AFB=78°,直接寫出∠DGB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解答
(1)如圖①,在正方形ABCD中,△AEF的頂點E,F分別在BC,CD邊上,高AG與正方形的邊長相等,求∠EAF的度數. 
(2)如圖②,在Rt△ABD中,∠BAD=90°,AB=AD,點M,N是BD邊上的任意兩點,且∠MAN=45°,將△ABM繞點A逆時針旋轉90°至△ADH位置,連接NH,試判斷MN,ND,DH之間的數量關系,并說明理由. 
(3)在圖①中,連接BD分別交AE,AF于點M,N,若EG=4,GF=6,BM=3 ![]() ,求AG,MN的長.
,求AG,MN的長. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】材料理解:如圖1點P,Q是標準體育場400m跑道上兩點,沿跑道從P到Q既可以逆時針,也可以順時針,我們把沿跑道從點P到點Q的順時針路程與逆時針路程的較小者叫P、Q兩點的最佳環距離.(如圖1,PQ順時針的路程為120m,逆時針的路程為280m,則PQ的最佳環距離為120m).
問題提出:一次校運動800m預決賽中,如圖2有甲、乙兩名運動員他們同時同地從點M處出發,勻速跑步,他們之間的最佳環距離y(m)與乙用的時間x(s)之間的函數關系如圖所示;解決以下問題:
(1)a=_________,乙的速度為___________.
(2)求線段BC的解析式,并寫出自變量的范圍.
(3)若本次運動會是1000m預決賽,甲完成比賽后是否有可能比乙多跑一圈,計算說明.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AC是正方形ABCD的對角線,將△ACD繞著點A順時針旋轉后得到△AC′D′,點D′落在AC上,C′D′交BC于點E,若AB=1,則圖中陰影部分圖形的面積是 . 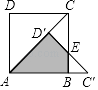
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們給出如下定義:順次連接任意一個四邊形各邊中點所得的四邊形叫中點四邊形.
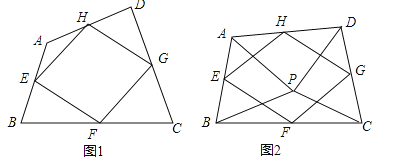
(1)如圖1,四邊形ABCD中,點E,F,G,H分別為邊AB,BC,CD,DA的中點.求證:中點四邊形EFGH是平行四邊形;
(2)如圖2,點P是四邊形ABCD內一點,且滿足PA=PB,PC=PD,∠APB=∠CPD,點E,F,G,H分別為邊AB,BC,CD,DA的中點,猜想中點四邊形EFGH的形狀,并證明你的猜想;
(3)若改變(2)中的條件,使∠APB=∠CPD=90°,其他條件不變,直接寫出中點四邊形EFGH的形狀.(不必證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=x的圖象為直線l.
(1)觀察與探究
已知點A與A′,點B與B′分別關于直線l對稱,其位置和坐標如圖所示.請在圖中標出C(4,﹣1)關于線l的對稱點C′的位置,并寫出C′的坐標_____;
(2)歸納與發現
觀察以上三組對稱點的坐標,你會發現:
平面直角坐標系中點P(a,b)關于直線l的對稱點P′的坐標為_____;
(3)運用與拓展
已知兩點M(﹣3,3)、N(﹣4,﹣1),試在直線l上作出點Q,使點Q到M、N兩點的距離之和最小,并求出相應的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
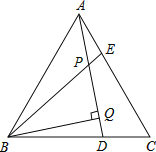
【題目】如圖,△ABC為等邊三角形,AE=CD,AD、BE相交于點P,BQ⊥AD于Q.
(1)求證:△ADC≌△BEA;
(2)若PQ=4,PE=1,求AD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com