
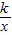 (k≠0)與△ABC有交點,則k的取值范圍是( )
(k≠0)與△ABC有交點,則k的取值范圍是( )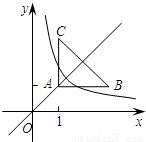
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源:2010年全國中考數學試題匯編《三角形》(11)(解析版) 題型:解答題
 x與拋物線y=ax2+b(a≠0)交于A(-4,-2),B(6,3)兩點.拋物線與y軸的交點為C.
x與拋物線y=ax2+b(a≠0)交于A(-4,-2),B(6,3)兩點.拋物線與y軸的交點為C. ?若存在,試求出此時點P的坐標;若不存在,請說明理由.
?若存在,試求出此時點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2010年全國中考數學試題匯編《二次函數》(08)(解析版) 題型:解答題
 x與拋物線y=ax2+b(a≠0)交于A(-4,-2),B(6,3)兩點.拋物線與y軸的交點為C.
x與拋物線y=ax2+b(a≠0)交于A(-4,-2),B(6,3)兩點.拋物線與y軸的交點為C. ?若存在,試求出此時點P的坐標;若不存在,請說明理由.
?若存在,試求出此時點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2010年四川省攀枝花市中考數學試卷(解析版) 題型:解答題
 x與拋物線y=ax2+b(a≠0)交于A(-4,-2),B(6,3)兩點.拋物線與y軸的交點為C.
x與拋物線y=ax2+b(a≠0)交于A(-4,-2),B(6,3)兩點.拋物線與y軸的交點為C. ?若存在,試求出此時點P的坐標;若不存在,請說明理由.
?若存在,試求出此時點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源:2008年全國中考數學試題匯編《反比例函數》(01)(解析版) 題型:選擇題
 (k≠0)與△ABC有交點,則k的取值范圍是( )
(k≠0)與△ABC有交點,則k的取值范圍是( )
查看答案和解析>>
科目:初中數學 來源:2009年全國中考數學試題匯編《三角形》(04)(解析版) 題型:選擇題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com