
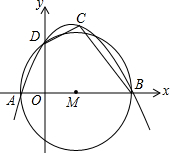
 如圖,⊙M的圓心M在x軸上,且與x軸分別交于A、B兩點與y軸的正半軸交于點D,點A、B的橫坐標分別是方程x2=3x+4的兩根,一條拋物線經過A、B、D三點,點C為第一象限拋物線上一動點.
如圖,⊙M的圓心M在x軸上,且與x軸分別交于A、B兩點與y軸的正半軸交于點D,點A、B的橫坐標分別是方程x2=3x+4的兩根,一條拋物線經過A、B、D三點,點C為第一象限拋物線上一動點.分析 (1)A(-1,0),B(4,0),可以假設拋物線為y=a(x+1)(x-4),連接BD,由△AOD∽△DOB,得OD2=AO•BO,推出OD=2,推出D(0,2),把D(0,2)代入y=a(x+1)(x-4)中,求出a即可.
(2)設四邊形ABCD面積為S,構建二次函數,利用二次函數的性質解決問題即可.
解答 解:(1)∵點A、B的橫坐標分別是方程x2=3x+4的兩根,
∴A(-1,0),B(4,0),
可以假設拋物線為y=a(x+1)(x-4),連接BD,
∵AB是直徑,
∴∠ADB=90°,
∵DO⊥AB,
∴∠AOD=∠DOB=90°,
∵∠ADO+∠DAO=90°,∠ADO+∠ODB=90°,
∴∠DAO=∠BDO,
∴△AOD∽△DOB,
∴OD2=AO•BO,
∴OD=2,
∴D(0,2),
把D(0,2)代入y=a(x+1)(x-4)中,得到a=-$\frac{1}{2}$,
∴拋物線的解析式為y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)連接OC.設C(m,-$\frac{1}{2}$m2+$\frac{3}{2}$m+2),
S=S△ADO+S△DCO+S△BCO=$\frac{1}{2}$×1×2+$\frac{1}{2}$×2×m+$\frac{1}{2}$×4×(-$\frac{1}{2}$m2+$\frac{3}{2}$m+2)=-(m-2)2+9,
∵-1<0,
∴m=2時,S有最大值,最大值為9.
點評 本題考查二次函數與x軸的交點、二次函數的最值問題、待定系數法等知識,解題的關鍵是學會根據二次函數解決最值問題,屬于中考常考題型.


科目:初中數學 來源: 題型:選擇題
| A. | 3個 | B. | 4個 | C. | 5個 | D. | 6個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com