
【題目】某農業觀光園將一塊面積為![]() 的觀光園分成
的觀光園分成![]() 三個區域,分別種植甲、乙、丙三種花卉,且每平方米栽種甲
三個區域,分別種植甲、乙、丙三種花卉,且每平方米栽種甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株.已知
株.已知![]() 區域的面積是
區域的面積是![]() 的
的![]() 倍,記A區域的面積為
倍,記A區域的面積為![]() 區域的面積為
區域的面積為![]() .
.
花卉 項目 | 甲 | 乙 | 丙 |
面積 |
|
| |
株/ |
|
|
|
數量 |
|
(1)完成上表(結果用含![]() 的代數式表示).
的代數式表示).
(2)若三種花卉共栽種![]() 株
株
①求![]() 與
與![]() 的值.
的值.
②若三種花卉的單價(都是整數)之和為![]() 元,全部栽種共需
元,全部栽種共需![]() 元,求種植面積最大的花卉總價.
元,求種植面積最大的花卉總價.
【答案】(1)見解析;(2)①![]() ,
,![]() ;②11200或5600元
;②11200或5600元
【解析】
(1)記A區域面積為x,則B區域面積是2x,根據每平方米栽種甲2株或乙4株,即可解答;
(2)①根據![]() 三個區域的總面積為
三個區域的總面積為![]() ,三種花卉共栽種
,三種花卉共栽種![]() 株,列二元一次方程組求解即可;
株,列二元一次方程組求解即可;
②設三種花卉的單價分別為a元、b元、c元,根據三種花卉的單價(都是整數)之和為![]() 元,全部栽種共需
元,全部栽種共需![]() 元,列出三元一次方程組,分析求解即可.
元,列出三元一次方程組,分析求解即可.
(1) 記A區域面積為x,則B區域面積是2x,
∵甲、乙、丙三種花卉,每平方米栽種甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株,
株,
∴甲花卉種植數量:2x,乙花卉種植數量:8x;
表如下:
花卉 項目 | 甲 | 乙 | 丙 |
面積 |
| 2x |
|
株/ |
|
|
|
數量 | 2x | 8x |
|
(2) ①根據題意列方程組:![]()
解方程組得:![]() ,
,
∴![]() ,
,![]() ;
;
②設三種花卉的單價分別為a元、b元、c元,
由(2)可知,分別種植甲、乙、丙三種花卉的株數為280株,1120株,1680株,
根據題意得:![]() ,
,
整理得:3b+5c=35,
∴b=10,c=1或b=5,c=4,
∵三種花卉的單價(都是整數)之和為40元,
∴a=29或a=31,
∴a=29,b=10,c=1或a=31,b=5,c=4,
由(2)可知乙種花卉種植280畝,面積最大,
∴種植面積最大的花卉總價為:280×4×10=11200(元)或280×4×5=5600(元)
答:種植面積最大的花卉總價為11200或5600元.


 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
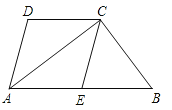
(1)求證:四邊形AECD是菱形;
(2)若點E是AB的中點,試判斷△ABC的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】暑假期間,小明一家到某拓展基地訓練,![]() 小明和他媽媽坐公交車先出發,爸爸在家整理物品,隨后爸爸自駕車沿著相同的道路后出發
小明和他媽媽坐公交車先出發,爸爸在家整理物品,隨后爸爸自駕車沿著相同的道路后出發![]() 他爸爸到拓展基地后,發現忘了東西在家里,于是立即返回家里取,取到東西后又馬上駕車前往拓展基地
他爸爸到拓展基地后,發現忘了東西在家里,于是立即返回家里取,取到東西后又馬上駕車前往拓展基地![]() 如圖是他們離家的距離s
如圖是他們離家的距離s![]() km
km![]() 與小明離家的時問t
與小明離家的時問t![]() 的關系圖.
的關系圖.
(1)請根據圖象,回答問題:
①圖中點A表示的意義是 .
②當爸爸第一次到達度假村后,小明離度假村的距離是______ km;
(2)爸爸在返回家的途中與小明相遇時,小明離家的距離是多少?
(3)整個運動過程中(雙方全部到達會合時,視為運動結束),請直接寫出小明與爸爸相距24km時t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線AB、CD相交于點O,OE平分∠BOD.OF⊥CD,垂足為O,若∠EOF=54°.
(1)求∠AOC的度數;
(2)作射線OG⊥OE,試求出∠AOG的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,現將一直角三角形
,現將一直角三角形![]() 放入圖中,其中
放入圖中,其中![]() ,
,![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]()
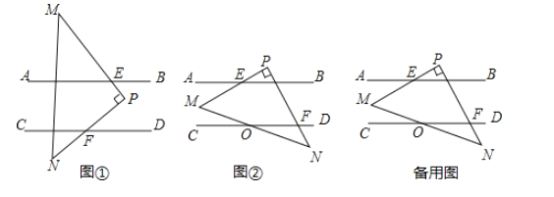
(1)當![]() 所放位置如圖①所示時,則
所放位置如圖①所示時,則![]() 與
與![]() 的數量關系為_______;請說明理由.
的數量關系為_______;請說明理由.
(2)當![]() 所放位置如圖②所示時,
所放位置如圖②所示時,![]() 與
與![]() 的數量關系為________;
的數量關系為________;
(3)在(2)的條件下,若![]() 與
與![]() 交于點0,且
交于點0,且![]() ,
,![]() ,求
,求![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
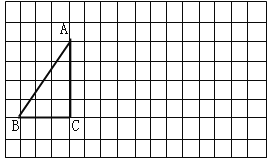
【題目】將下列方格紙中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)畫出平移后的三角形;
.(1)畫出平移后的三角形;
(2)若AB=5,則![]() = .
= .
(3)連接AA1,BB1, 根據“圖形平移”的性質,得:線段AA1與線段BB1的數量關系和位置關系是: .
(4)求圖中∠![]() AC+∠
AC+∠![]() BC的度數.
BC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學家華羅庚在一次出國訪問途中,看到飛機上鄰座的乘客閱讀的雜志上有一道智力題:求59319的立方根.華羅庚脫口而出:39.眾人感覺十分驚奇,請華羅庚給大家解讀其中的奧秘.
你知道怎樣迅速準確的計算出結果嗎?請你按下面的問題試一試:
①![]() ,又
,又![]() ,
,
![]() ,∴能確定59319的立方根是個兩位數.
,∴能確定59319的立方根是個兩位數.
②∵59319的個位數是9,又![]() ,∴能確定59319的立方根的個位數是9.
,∴能確定59319的立方根的個位數是9.
③如果劃去59319后面的三位319得到數59,
而![]() ,則
,則![]() ,可得
,可得![]() ,
,
由此能確定59319的立方根的十位數是3
因此59319的立方根是39.
(1)現在換一個數195112,按這種方法求立方根,請完成下列填空.
①它的立方根是_______位數.
②它的立方根的個位數是_______.
③它的立方根的十位數是__________.
④195112的立方根是________.
(2)請直接填寫結果:
①![]() ________.
________.
②![]() ________.
________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某外資企業生產的一批產品上市后30天內全部售完,該企業對這批產品上市后每天的銷售情況進行了跟蹤調查.其中,國內市場的日銷售量y1(萬件)與時間t(t為整數,單位:天)的部分對應值如下表所示.而國外市場的日銷售量y2(萬件)與時間t(t為整數,單位:天)的關系如圖所示.
(1)請你從所學過的一次函數、二次函數和反比例函數中確定哪種函數能表示y1與t的變化規律,寫出y1與t的函數關系式及自變量t的取值范圍;
(2)分別探求該產品在國外市場上市20天前(不含第20天)與20天后(含第20天)的日銷售量y2與時間t所符合的函數關系式,并寫出相應自變量t的取值范圍;
(3)設國內、外市場的日銷售總量為y萬件,寫出y與時間t的函數關系式,并判斷上市第幾天國內、外市場的日銷售總量y最大,并求出此時的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
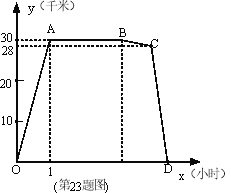
【題目】(2011福建龍巖,23, 12分) 周六上午8:00小明從家出發,乘車1小時到郊外某基地參加社會實踐活動,在基地活動2.2小時后,因家里有急事,他立即按原路以4千米/時的平均速度步行返回.同時爸爸開車從家出發沿同一路線接他,在離家28千米處與小明相遇。接到小明后保持車速不變,立即按原路返回.設小明離開家的時間為x小時,小名離家的路程y (干米) 與x (小時)之間的函致圖象如圖所示,
(1)小明去基地乘車的平均速度是________千米/小時,爸爸開車的平均速度應是________千米/小時;
(2)求線段CD所表示的函斂關系式;
(3)問小明能否在12:0 0前回到家?若能,請說明理由:若不能,請算出12:00時他離家的路程,
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com