
【題目】已知:在矩形![]() 和
和![]() 中,
中,![]() ,
,![]() .
.

(1)如圖1,當點![]() 在對角線
在對角線![]() 上,點
上,點![]() 在
在![]() 邊上時,連接
邊上時,連接![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,則
,則![]() 與
與![]() 的數量關系是_____,
的數量關系是_____,![]() _____
_____![]() ;
;
(2)如圖2,將圖1中的![]() 繞點
繞點![]() 旋轉,使點
旋轉,使點![]() 在
在![]() 的延長線上,(1)中的其他條件不變.
的延長線上,(1)中的其他條件不變.
①(1)中![]() 與
與![]() 的數量關系仍然成立嗎?請證明你的結論;
的數量關系仍然成立嗎?請證明你的結論;
②求![]() 的度數.
的度數.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
(1)根據直角三角形斜邊上中線性質得ME=MD,根據含有30°的直角三角形性質∠EMC=∠EMF+∠CMF=2(∠MDE+∠MDC)=2∠BDC,由∠DBC=30°,得∠BDC=90°-30°=60°,∠EMC=2∠BDC=2×60°=120°;(2)①分別延長EM,CD交于點G,根據矩形性質證△FEM≌△DGM,得ME=GM,在Rt△GEC中,MC=![]() EG=ME;②如圖3,分別延長FE,DB交于點H,證△FEB≌△HEB.得FE=HE.根據EM∥HD,得∠7=∠4=30°,∠7=∠8=30°,∠EMC=180°-∠7-∠8=180°-30°-30°=120°.
EG=ME;②如圖3,分別延長FE,DB交于點H,證△FEB≌△HEB.得FE=HE.根據EM∥HD,得∠7=∠4=30°,∠7=∠8=30°,∠EMC=180°-∠7-∠8=180°-30°-30°=120°.
(1)如圖1,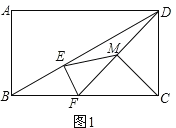 ,
,
∵∠BEF=90°,
∴∠DEF=90°,
∵點M是DF的中點,
∴ME=MD,
∵∠BCD=90°,點M是DF的中點,
∴MC=MD,
∴ME=MC;
∵ME=MD,
∴∠MDE=∠MED,
∴∠EMF=∠MDE+∠MED=2∠MDE,
∵MC=MD,
∴∠MDC=∠MCD,
∴∠CMF=∠MDC+∠MCD=2∠MDC,
∴∠EMC=∠EMF+∠CMF=2(∠MDE+∠MDC)=2∠BDC,
又∵∠DBC=30°,
∴∠BDC=90°-30°=60°,
∴∠EMC=2∠BDC=2×60°=120°.
(2)①ME=MC仍然成立.
證明:如圖2,分別延長EM,CD交于點G, ,
,
∵四邊形ABCD是矩形,
∴∠DCB=90°.
∵∠BEF=90°,
∴∠FEB+∠DCB=180°.
∵點E在CB的延長線上,
∴FE∥DC.
∴∠1=∠G.
∵M是DF的中點,
∴FM=DM.
在△FEM和△DGM中,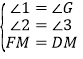 ,
,
∴△FEM≌△DGM,
∴ME=GM,
∴在Rt△GEC中,
MC=![]() EG=ME,
EG=ME,
∴ME=MC.
②如圖3,分別延長FE,DB交于點H,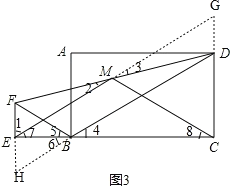 ,
,
∵∠4=∠5,∠4=∠6,
∴∠5=∠6.
∵點E在直線FH上,∠FEB=90°,
∴∠HEB=∠FEB=90°.
在△FEB和△HEB中,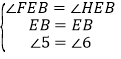 ,
,
∴△FEB≌△HEB.
∴FE=HE.
∵FM=MD,
∴EM是三角形FHD的中位線,
∴EM∥HD,
∴∠7=∠4=30°,
∵ME=MC,
∴∠7=∠8=30°,
∴∠EMC=180°-∠7-∠8=180°-30°-30°=120°.
故答案為:ME=MC,120.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:
【題目】圓上有五個點,這五個點將圓分成五等份(每一份稱為一段弧長),把這五個點按順時針方向依次編號為1,2,3,4,5,若從某一點開始,沿圓周順時針方向行走,點的編號是數字幾,就走幾段弧長,則稱這種走法為一次“移位”.如:小明在編號為3的點,那么他應走3段弧長,即從3→ 4→5→1為第一次“移位”,這時他到達編號為1的點,然后從1→2為第二次“移位”.若小明從編號為4的點開始,第2020次“移位”后,他到達編號為______的點.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個不透明的紙箱里裝有紅、黃、藍三種顏色的小球,它們除顏色外完全相同,其中紅球有2 個,黃球有1個,藍球有1個.現有一張電影票,小明和小亮決定通過摸球游戲定輸贏,贏的一方得電影票.
(1)游戲規則1:兩人各摸1個球,先由小明從紙箱里隨機摸出1個球,記錄顏色后放回,將小球搖勻,再由小亮隨機摸出1個球.若兩人摸到的球顏色相同,則小明贏,否則小亮贏.這個游戲規則對雙方公平嗎?請你利用樹狀圖或列表法說明理由.
(2)游戲規則2; 兩人同時各摸1個球,若兩人摸到的球顏色相同,則小明贏,否則小亮贏.這個游戲小明贏得電影票的概率為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題呈現:如圖1,點E、F、G、H分別在矩形ABCD的邊AB、BC、CD、DA上,AE=DG,求證:2S四邊形EFGH=S矩形ABCD.(S表示面積)
實驗探究:某數學實驗小組發現:若圖1中AH≠BF,點G在CD上移動時,上述結論會發生變化,分別過點E、G作BC邊的平行線,再分別過點F、H作AB邊的平行線,四條平行線分別相交于點A1、B1、C1、D1,得到矩形A1B1C1D1.
如圖2,當AH>BF時,若將點G向點C靠近(DG>AE),經過探索,發現:2S四邊形EFGH=S矩形ABCD+![]() .
.
如圖3,當AH>BF時,若將點G向點D靠近(DG<AE),請探索S四邊形EFGH、S矩形ABCD與![]() 之間的數量關系,并說明理由.
之間的數量關系,并說明理由.
遷移應用:
請直接應用“實驗探究”中發現的結論解答下列問題:
如圖4,點E、F、G、H分別是面積為25的正方形ABCD各邊上的點,已知AH>BF,AE>DG,S四邊形EFGH=11,HF=![]() ,求EG的長.
,求EG的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中的每個小正方形的邊長都是1,每個小格的頂點叫做格點.
(1)在圖1中以格點為頂點畫一個面積為10的正方形;
(2)在圖2中以格點為頂點畫一個三角形,使三角形三邊長分別為2、![]() 、
、![]() ;
;
(3)如圖3,點A、B、C是小正方形的頂點,求∠ABC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,直線l1、l2、l3分別通過A、B、C三點,且l1∥l2∥l3,若l1與l2的距離為6,正方形ABCD的面積等于100,l2與l3的距離為( )

A. 8B. 10C. 9D. 7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A(1,0),B(0,2),以AB為邊在第一象限內作正方形ABCD,直線CD與y軸交于點G,再以DG為邊在第一象限內作正方形DEFG,若反比例函數![]() 的圖像經過點E,則k的值是 ( )
的圖像經過點E,則k的值是 ( )

(A)33 (B)34 (C)35 (D)36
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知菱形ABCD的對角線相交于點O,延長AB至點E,使BE=AB,連接CE.

(1)求證:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某港口![]() 位于東西方向的海岸線上,“遠航”號、“海天”號輪船同時離開港口,各自沿一固定方向航行,“遠航”號每小時航行
位于東西方向的海岸線上,“遠航”號、“海天”號輪船同時離開港口,各自沿一固定方向航行,“遠航”號每小時航行![]() “海天”號每小時航行
“海天”號每小時航行![]() ,它們離開港口兩個小時后,“遠航”號到達
,它們離開港口兩個小時后,“遠航”號到達![]() 處,“海天”到達
處,“海天”到達![]() 處,
處,![]() 相距
相距![]() ,且知道“遠航”號沿東北方向航行,那么“海天”號沿什么方向航行?
,且知道“遠航”號沿東北方向航行,那么“海天”號沿什么方向航行?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com