
【題目】對于平面直角坐標系xOy中的點P和⊙C,給出如下定義:若存在過點P的直線l交⊙C于異于點P的A,B兩點,在P,A,B三點中,位于中間的點恰為以另外兩點為端點的線段的中點時,則稱點P為⊙C 的相鄰點,直線l為⊙C關于點P的相鄰線.
(1)當⊙O的半徑為1時,
①分別判斷在點D( ![]() ,
, ![]() ),E(0,﹣
),E(0,﹣ ![]() ),F(4,0)中,是⊙O的相鄰點有;
),F(4,0)中,是⊙O的相鄰點有;
②請從①中的答案中,任選一個相鄰點,在圖1中做出⊙O關于它的一條相鄰線,并說明你的作圖過程;
③點P在直線y=﹣x+3上,若點P為⊙O的相鄰點,求點P橫坐標的取值范圍;
(2)⊙C的圓心在x軸上,半徑為1,直線y=﹣ ![]() 與x軸,y軸分別交于點M,N,若線段MN上存在⊙C的相鄰點P,直接寫出圓心C的橫坐標的取值范圍.
與x軸,y軸分別交于點M,N,若線段MN上存在⊙C的相鄰點P,直接寫出圓心C的橫坐標的取值范圍.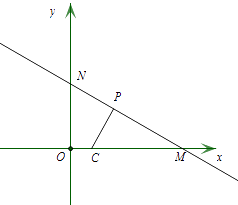
【答案】
(1)D或E,解:②連接OD,過點D作OD的垂線交⊙O于A、B兩點,如圖所示: 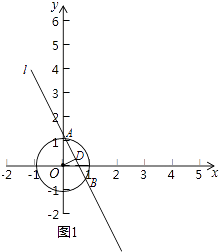 ,③令x=0代入y=﹣x+3,∴y=3,令y=0代入y=﹣x+3,∴x=3,∴y=﹣x+3與坐標軸的交點為(0,3)和(3,0)∵由于點P在直線y=﹣x+3上,且點P是⊙O的相鄰點,∴0≤PO≤3,且PO≠1又∵點P在⊙O外,∴1<PO≤3,∴p的橫坐標范圍為:0≤x≤3;
,③令x=0代入y=﹣x+3,∴y=3,令y=0代入y=﹣x+3,∴x=3,∴y=﹣x+3與坐標軸的交點為(0,3)和(3,0)∵由于點P在直線y=﹣x+3上,且點P是⊙O的相鄰點,∴0≤PO≤3,且PO≠1又∵點P在⊙O外,∴1<PO≤3,∴p的橫坐標范圍為:0≤x≤3;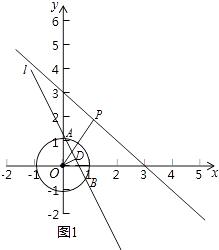
(2)解:令x=0代入y=﹣ ![]() x+2
x+2 ![]() ,
,
∴y=2 ![]() ,
,
∴N(0,2 ![]() ),
),
令y=0代入y=﹣ ![]() x+2
x+2 ![]() ,
,
∴x=6,
∴M(6,0),
∵點P是半徑為1的⊙C的相鄰點,
∴0≤PC≤3且PC≠1,
∴點C在以點P為圓心,半徑為3的圓內,且不能在以點P為圓心,半徑為1的圓上,
∵點C在x軸上,
∴點C的橫坐標范圍的取值范圍:0≤x≤9.
【解析】解:(1)由定義可知,
當點P在⊙C內時,
由垂徑定理可知,點P必為⊙C的相鄰點,
此時,0≤PC<1;
當點P在⊙C外時,
設點A是PB的中點,
連接PC交⊙C于點M,
延長PC交⊙C于點N,
連接AM,BN,

∵∠AMP+∠NMA=180°,
∠B+∠NMA=180°,
∴∠AMP=∠B,
∵∠P=∠P,
∴△AMP∽△NBP,
∴ ![]() =
= ![]() ,
,
∴PAPB=PMPN,
∵點A是PB的中點,
∴AB=PA,
又∵⊙C的半徑為1,
∴2AB2=(PC﹣CM)(PC+CN),
∴2AB2=PC2﹣1,
又∵AB是⊙C的弦,
∴AB≤2,
∴2AB2≤8,
∴PC2﹣1≤8,
∴PC2≤9,
∴PC≤3,
∵點P在⊙C外,
∴PC>1,
∴1<PC≤3,
當點P在⊙C上時,
此時PC=1,但不符合題意,
綜上所述,半徑為1的⊙C,當點P與圓心C的距離滿足:0≤PC≤3,且PC≠1時,點P為⊙C的相鄰點;
①∵D( ![]() ,
, ![]() ),
),
∴DO= ![]() =
= ![]() ,
,
∵E(0,﹣ ![]() ),
),
∴OE= ![]() ,
,
∵F(4,0),
∴OF=4,
∴D和E是⊙O的相鄰點;


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
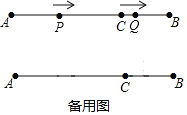
【題目】如圖,AB=12cm,點C在線段AB上,AC=3BC,動點P從點A出發,以4cm/s的速度向右運動,到達點B之后立即返回,以4cm/s的速度向左運動;動點Q從點C出發,以1cm/s的速度向右運動,到達點B之后立即返回,以1cm/s的速度向左運動.設它們同時出發,運動時間為t秒,當第二次重合時,P、Q兩點停止運動.
(1)AC=______cm,BC=______cm;
(2)當t=______秒時,點P與點Q第一次重合;當t=______秒時,點P與點Q第二次重合;
(3)當t為何值時,AP=PQ?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數 ![]() 的圖像經過點
的圖像經過點 ![]() .
.
(1)求這個二次函數的函數解析式;
(2)若拋物線交x軸于A,B兩點,交y軸于C點,頂點為D,求以A、B、C、D為頂點的四邊形面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
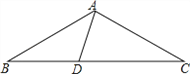
【題目】(10分)如圖,在△ABC中,AB=AC,D為BC上一點,∠B=30°,連接AD.
(1)若∠BAD=45°,求證:△ACD為等腰三角形;
(2)若△ACD為直角三角形,求∠BAD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
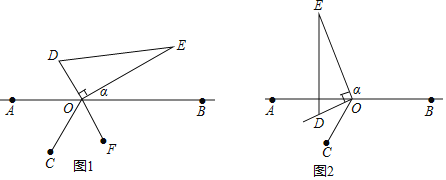
【題目】如圖1,點A、O、B在同一直線上,∠AOC=60°,在直線AB另一側,直角三角形DOE繞直角頂點O逆時針旋轉(當OD與OC重合時停止),設∠BOE=α:
(1)如圖1,當DO的延長線OF平分∠BOC,∠α=______度;
(2)如圖2,若(1)中直角三角形DOE繼續逆時針旋轉,當OD位于∠AOC的內部,且∠AOD=![]() ∠AOC,∠α=__度;
∠AOC,∠α=__度;
(3)在上述直角三角形DOE的旋轉過程中,(∠COD+∠α)的度數是否改變?若不改變,請求出其度數;若改變,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為測量操場上旗桿的高度,小麗同學想到了物理學中平面鏡成像的原理,她拿出隨身攜帶的鏡子和卷尺,先將鏡子放在腳下的地面上,然后后退,直到她站直身子剛好能從鏡子里看到旗桿的頂端E,標記好腳掌中心位置為B,測得腳掌中心位置B到鏡面中心C的距離是50cm,鏡面中心C距離旗桿底部D的距離為4m,如圖所示.已知小麗同學的身高是1.54m,眼睛位置A距離小麗頭頂的距離是4cm,則旗桿DE的高度等于( ) 
A.10m
B.12m
C.12.4m
D.12.32m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【新知理解】
如圖①,點C在線段AB上,圖中共有三條線段AB、AC和BC,若其中有一條線段的長度是另外一條線段長度的2倍,則稱點C是線段AB的“巧點”.
線段的中點__________這條線段的“巧點”;(填“是”或“不是”).
若AB = 12cm,點C是線段AB的巧點,則AC=___________cm;
【解決問題】
(3) 如圖②,已知AB=12cm.動點P從點A出發,以2cm/s的速度沿AB向點B勻速移動:點Q從點B出發,以1cm/s的速度沿BA向點A勻速移動,點P、Q同時出發,當其中一點到達終點時,運動停止,設移動的時間為t(s).當t為何值時,A、P、Q三點中其中一點恰好是另外兩點為端點的線段的巧點?說明理由

![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
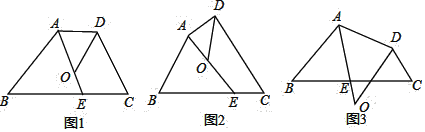
【題目】四邊形ABCD中,∠BAD的角平分線與邊BC交于點E,∠ADC的角平分線交直線AE于點O.
(1)若點O在四邊形ABCD的內部,
①如圖1,若AD∥BC,∠B=40°,∠C=70°,則∠DOE= °;
②如圖2,試探索∠B、∠C、∠DOE之間的數量關系,并將你的探索過程寫下來.
(2)如圖3,若點O在四邊形ABCD的外部,請你直接寫出∠B、∠C、∠DOE之間的數量關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com