
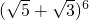 的最大整數是 ________.
的最大整數是 ________.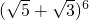 =
=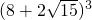 ,然后利用換元法設令
,然后利用換元法設令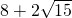 =a,
=a,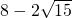 =b;經計算知,a,b是方程x2-16x+4=0的兩個根,然后根據根與系數是關系解得a3、b3;再利用立方差公式解得a3+b3=16(a2+b2)-4(a+b)=3904,利用b的取值范圍來解答問題.
=b;經計算知,a,b是方程x2-16x+4=0的兩個根,然后根據根與系數是關系解得a3、b3;再利用立方差公式解得a3+b3=16(a2+b2)-4(a+b)=3904,利用b的取值范圍來解答問題.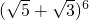 =
=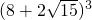 ,
,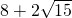 =a,
=a,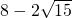 =b,
=b,

 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com