
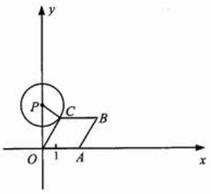
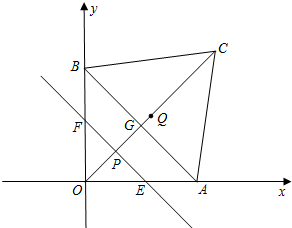
如圖,已知點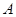 從
從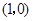 出發,以1個單位長度/秒的速度沿
出發,以1個單位長度/秒的速度沿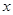 軸向正方向運動,以
軸向正方向運動,以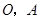 為頂點作菱形
為頂點作菱形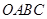 ,使點
,使點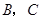 在第一象限內,且
在第一象限內,且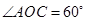 ;以
;以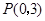 為圓心,
為圓心, 為半徑作圓.設點
為半徑作圓.設點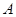 運動了
運動了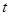 秒,求:
秒,求:
(1)點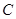 的坐標(用含
的坐標(用含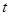 的代數式表示);
的代數式表示);
(2)當點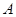 在運動過程中,所有使
在運動過程中,所有使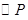 與菱形
與菱形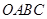 的邊所在直線相切的
的邊所在直線相切的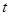 的值.
的值.
解:(1)過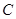 作
作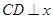 軸于
軸于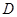 ,
,
 ,
,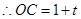 ,
,
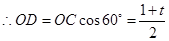 ,
,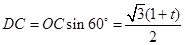 ,
,
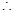 點
點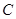 的坐標為
的坐標為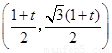 .
.
(2)①當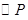 與
與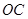 相切時(如圖1),切點為
相切時(如圖1),切點為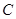 ,此時
,此時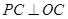 ,
,
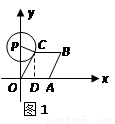
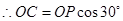 ,
, ,
,
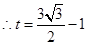 .
.
②當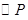 與
與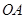 ,即與
,即與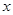 軸相切時(如圖2),則切點為
軸相切時(如圖2),則切點為 ,
, ,
,
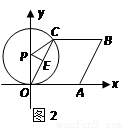
過 作
作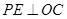 于
于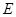 ,則
,則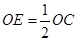 ,
,
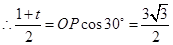 ,
,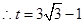 .
.
③當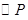 與
與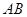 所在直線相切時(如圖3),設切點為
所在直線相切時(如圖3),設切點為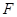 ,
,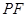 交
交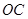 于
于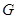 ,
,
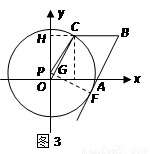
則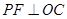 ,
,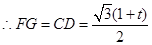 ,
,
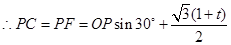 .
.
過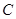 作
作 軸于
軸于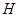 ,則
,則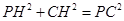 ,
,
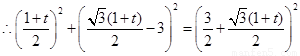 ,
,
化簡,得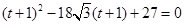 ,
,
解得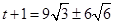 ,
,
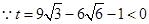 ,
,
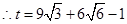 .
.
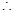 所求
所求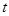 的值是
的值是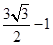 ,
,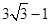 和
和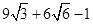 .
.
【解析】(1)過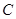 作
作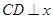 軸于
軸于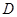 ,利用三角函數求得OD、DC的長,從而求得點
,利用三角函數求得OD、DC的長,從而求得點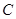 的坐標
的坐標
⊙P與菱形OABC的邊所在直線相切,則可與OC相切;或與OA相切;或與AB相切,應分三種情況探討:①當圓P與OC相切時,如圖1所示,由切線的性質得到PC垂直于OC,再由OA=+t,根據菱形的邊長相等得到OC=1+t,由∠AOC的度數求出∠POC為30°,在直角三角形POC中,利用銳角三角函數定義表示出cos30°=oc/op,表示出OC,
等于1+t列出關于t的方程,求出方程的解即可得到t的值;②當圓P與OA,即與x軸相切時,過P作PE垂直于OC,又PC=PO,利用三線合一得到E為OC的中點,OE為OC的一半,而OE=OPcos30°,列出關于t的方程,求出方程的解即可得到t的值;③當圓P與AB所在的直線相切時,設切點為F,PF與OC交于點G,由切線的性質得到PF垂直于AB,則PF垂直于OC,由CD=FG,在直角三角形OCD中,利用銳角三角函數定義由OC表示出CD,即為FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根據PF=PC,表示出PC,過C作CH垂直于y軸,在直角三角形PHC中,利用勾股定理列出關于t的方程,求出方程的解即可得到t的值,綜上,得到所有滿足題意的t的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
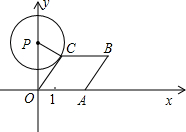 A為頂點作菱形OABC,使點B,C在第一象限內,且∠AOC=60°;以P(0,3)為圓心,PC為半徑作圓.設點A運動了t秒,求:
A為頂點作菱形OABC,使點B,C在第一象限內,且∠AOC=60°;以P(0,3)為圓心,PC為半徑作圓.設點A運動了t秒,求:查看答案和解析>>
科目:初中數學 來源: 題型:
| 2 |
| 7 |
| 2 |
| 2 |
| 7 |
| 2 |
| 2 |
 1個單位的速度從O運動到C,過P作直線EF∥AB分別交OA,OB于E,F.解答下列問題:
1個單位的速度從O運動到C,過P作直線EF∥AB分別交OA,OB于E,F.解答下列問題:查看答案和解析>>
科目:初中數學 來源:2008年初中畢業升學考試(江蘇無錫卷)數學(帶解析) 題型:解答題
如圖,已知點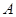 從
從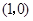 出發,以1個單位長度/秒的速度沿
出發,以1個單位長度/秒的速度沿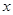 軸向正方向運動,以
軸向正方向運動,以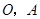 為頂點作菱形
為頂點作菱形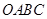 ,使點
,使點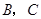 在第一象限內,且
在第一象限內,且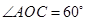 ;以
;以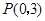 為圓心,
為圓心,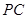 為半徑作圓.設點
為半徑作圓.設點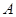 運動了
運動了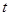 秒,求:
秒,求:
(1)點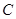 的坐標(用含
的坐標(用含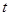 的代數式表示);
的代數式表示);
(2)當點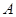 在運動過程中,所有使
在運動過程中,所有使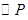 與菱形
與菱形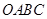 的邊所在直線相切的
的邊所在直線相切的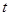 的值.
的值.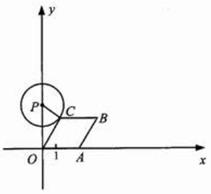
查看答案和解析>>
科目:初中數學 來源: 題型:
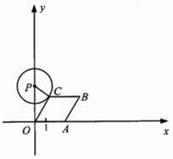
如圖,已知點![]() 從
從![]() 出發,以1個單位長度/秒的速度沿
出發,以1個單位長度/秒的速度沿![]() 軸向正方向運動,以
軸向正方向運動,以![]() 為頂點作菱形
為頂點作菱形![]() ,使點
,使點![]() 在第一象限內,且
在第一象限內,且![]() ;以
;以![]() 為圓心,
為圓心,![]() 為半徑作圓.設點
為半徑作圓.設點![]() 運動了
運動了![]() 秒,求:
秒,求:
(1)點![]() 的坐標(用含
的坐標(用含![]() 的代數式表示);
的代數式表示);
(2)當點![]() 在運動過程中,所有使⊙
在運動過程中,所有使⊙![]() 與菱形
與菱形![]() 的邊所在直線相切的
的邊所在直線相切的![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com