Question

已知：如圖， AF平分∠BAC，BC⊥AF， 垂足為E，點D與點A關于點E對稱，PB分別與線段CF，AF相交于P，M．

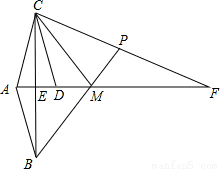
（1）求證：AB=CD；

（2）若∠BAC=2∠MPC，請你判斷∠F與∠MCD的數量關系，并說明理由．

Answer 1

（1）證明見解析；（2）∠F=∠MCD，理由見解析.

【解析】

試題分析：（1）由點D與點A關于點E對稱易證AC=CD，再根據角平分線，及垂直得到AC=AB，可得答案AB=CD；

（2）易證∠CAD=∠CDA=∠MPC，∠CMA=∠BMA=PMF，可得到∠MCD=∠F．

試題解析：（1）證明：∵AF平分∠BAC，

∴∠CAD=∠DAB=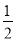∠BAC，

∵D與A關于E對稱，

∴E為AD中點，

∵BC⊥AD，

∴BC為AD的中垂線，

∴AC=CD．

在Rt△ACE和Rt△ABE中，（注：證全等也可得到AC=CD）

∠CAD+∠ACE=∠DAB+∠ABE=90°，∠CAD=∠DAB，

∴∠ACE=∠ABE，

∴AC=AB（注：證全等也可得到AC=AB），

∴AB=CD．

（2）【解析】
∠F=∠MCD，理由如下：

∵∠BAC=2∠MPC，

又∵∠BAC=2∠CAD，

∴∠MPC=∠CAD，

∵AC=CD，

∴∠CAD=∠CDA，

∴∠MPC=∠CDA，

∴∠MPF=∠CDM，

∵AC=AB，AE⊥BC，

∴CE=BE（注：證全等也可得到CE=BE），

∴AM為BC的中垂線，

∴CM=BM．（注：證全等也可得到CM=BM）

∵EM⊥BC，

∴EM平分∠CMB（等腰三角形三線合一）．

∴∠CME=∠BME（注：證全等也可得到∠CME=∠BME．），

∵∠BME=∠PMF，

∴∠PMF=∠CME，

∴∠MCD=∠F．（注：證三角形相似也可得到∠MCD=∠F）

考點：1.軸對稱的性質；2.線段垂直平分線的性質；3.等腰三角形的性質．