
【題目】如圖,P是直徑AB上的一點,AB=6,CP⊥AB交半圓![]() 于點C,以BC為直角邊構造等腰Rt△BCD,∠BCD=90°,連接OD.
于點C,以BC為直角邊構造等腰Rt△BCD,∠BCD=90°,連接OD.

小明根據學習函數的經驗,對線段AP,BC,OD的長度之間的關系進行了探究.
下面是小明的探究過程,請補充完整:
(1)對于點P在AB上的不同位置,畫圖、測量,得到了線段AP,BC,OD的長度的幾組值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置… | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | … |
BC | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | … |
OD | 6.71 | 7.24 | 7.07 | 6.71 | 6.16 | 5.33 | … |
在AP,BC,OD的長度這三個量中,確定________的長度是自變量,________的長度和________的長度都是這個自變量的函數;
(2)在同一平面直角坐標系xOy中,畫出(1)中所確定的函數的圖象;

(3)結合函數圖象,解決問題:當OD=2BC時,線段AP的長度約為________.
【答案】(1)AP,BC,OD或BC,AP,OD;(2)如圖1或圖2所示:見解析;(3)線段AP的長度約為4.5.
【解析】
(1)由函數的自變量及函數的定義即可得出答案;
(2)利用描點法畫出圖象即可.
(3)由數形結合的思想,直接觀察圖象,由x=4.5時所對應的兩個函數值即可發現此時OD=2BC.
(1) 由表格可確定BC隨著AP的變化而變化,BD隨著BC的變化而變化,故AP、BC的長度是自變量,OD或BC的長度和AP,OD的長度都是這個自變量的函數;
故答案為:AP,BC,OD或BC,AP,OD;在AP,BC,OD
(2)如圖1或圖2所示:
|
|
圖1 | 圖2 |
(3)由表格可知:當AP=4時,BC=3.46,OD=6.16; 當AP=4時,BC=2.45,OD=5.33,
∴當OD=2BC時
由可知線段AP的長度約為4.5.
|
|
圖3 | 圖4 |


 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,二次函數![]() 的圖象與x軸交于點A,B(點A在點B的左側),與y軸交于點C,頂點為P.
的圖象與x軸交于點A,B(點A在點B的左側),與y軸交于點C,頂點為P.
(1)直接寫出點A,C,P的坐標.
(2)畫出這個函數的圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象交x軸于(-1,0)點,則下列結論中正確的是( )

A.c<0B.a-b+c<0C.b2<4acD.2a+b=0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是一個可以自由轉動的轉盤,轉盤被分成面積相等的三個扇形,每個扇形上分別標上![]() ,1,-1三個數字.小明轉動轉盤,小亮猜結果,如果轉盤停止后指針指向的結果與小亮所猜的結果相同,則小亮獲勝,否則小明獲勝.
,1,-1三個數字.小明轉動轉盤,小亮猜結果,如果轉盤停止后指針指向的結果與小亮所猜的結果相同,則小亮獲勝,否則小明獲勝.
(1)如果小時轉動轉盤一次,小亮猜的結果是“正數”,那么小亮獲勝的概率是 .
(2)如果小明連續轉動轉盤兩次,小亮猜兩次的結果都是“正數”,請用畫樹狀圖或列表法求出小亮獲勝的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a,b,c是常數,a≠0)的自變量x與函數值y的部分對應值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y=ax2+bx+c | … | t | m | -2 | -2 | n | … |
根據以上列表,回答下列問題:
(1)直接寫出c的值和該二次函數圖象的對稱軸;
(2)寫出關于x的一元二次方程ax2+bx+c=t的根;
(3)若m=-1,求此二次函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
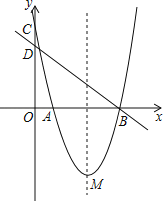
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c與兩坐標軸分別交于點A、B、C,直線y=﹣![]() x+4經過點B,與y軸交點為D,M(3,﹣4)是拋物線的頂點.
x+4經過點B,與y軸交點為D,M(3,﹣4)是拋物線的頂點.
(1)求拋物線的解析式.
(2)已知點N在對稱軸上,且AN+DN的值最小.求點N的坐標.
(3)在(2)的條件下,若點E與點C關于對稱軸對稱,請你畫出△EMN并求它的面積.
(4)在(2)的條件下,在坐標平面內是否存在點P,使以A、B、N、P為頂點的四邊形是平行四邊形?若存在,請直接寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
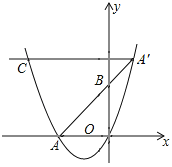
【題目】如圖,在平面直角坐標系中,拋物線y=x2+mx交x軸的負半軸于點A.點B是y軸正半軸上一點,點A關于點B的對稱點A′恰好落在拋物線上.過點A′作x軸的平行線交拋物線于另一點C.若點A′的橫坐標為1,則A′C的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c的頂點為D(﹣1,2),與x軸的一個交點A在點(﹣3,0)和(﹣2,0)之間,其部分圖象如圖,則以下結論:①b2﹣4ac<0;②當x>﹣1時,y隨x增大而減小;③a+b+c<0;④若方程ax2+bx+c﹣m=0沒有實數根,則m>2; ⑤3a+c<0.其中正確結論的個數是( )

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com