
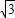 ,3),E(
,3),E(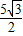 ,0)及原點O(0,0).
,0)及原點O(0,0).
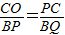 ,用Q點的坐標表示出BP、BQ的長,根據線段的比例關系式即可求出Q點的坐標.
,用Q點的坐標表示出BP、BQ的長,根據線段的比例關系式即可求出Q點的坐標.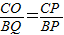 ,方法同①
,方法同①
 ,b=
,b=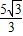 ,c=0.
,c=0. x2+
x2+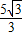 x.
x.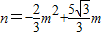 ,
,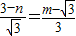 ,即
,即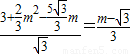 ,
,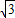 ,m2=
,m2=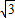 .
.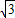 時,n=2,
時,n=2,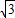 ,2)
,2)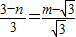 ,即
,即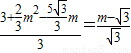
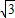 ,m2=
,m2=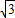 ,
,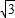 時,即為P點,
時,即為P點,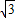 時,n=-3,
時,n=-3,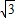 ,-3).
,-3).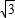 ,2),(3
,2),(3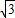 ,-3).
,-3).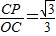 .
.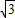 ,2)時,∠BPQ=∠COP=30度.
,2)時,∠BPQ=∠COP=30度.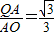 .
.

科目:初中數學 來源:2006年全國中考數學試題匯編《二次函數》(06)(解析版) 題型:解答題
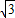 ,3),E(
,3),E(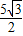 ,0)及原點O(0,0).
,0)及原點O(0,0).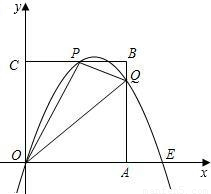
查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《二次函數》(09)(解析版) 題型:解答題
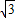 ,3),E(
,3),E( ,0)及原點O(0,0).
,0)及原點O(0,0).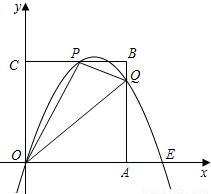
查看答案和解析>>
科目:初中數學 來源:2007年全國中考數學試題匯編《二次函數》(08)(解析版) 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2007年遼寧省大連市旅順口區中考數學試卷(解析版) 題型:解答題
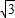 ,3),E(
,3),E(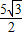 ,0)及原點O(0,0).
,0)及原點O(0,0).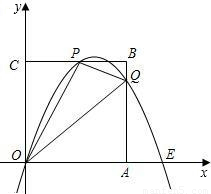
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com