甲,乙兩輛汽車同時從同一地點A出發,沿同一方向直線行駛,每輛車最多只能帶240L汽油,途中不能再加油,每升油可使一輛車前進12km,兩車都必須沿原路返回出發點,但是兩車相互可借用對方的油.請你設計一種方案,使其中一輛車盡可能地遠離出發地點A,并求出這輛車一共行駛了多少千米?
【答案】
分析:本題中由于兩車相互借對方的油,那么他們所走的距離和≤240×12×2,他們所走的距離差≤240×12.由此可得出自變量的取值范圍.
如果要讓一輛車盡可能的遠離A地并同時返回,那么就必須讓一輛車行駛一段后,把油給對方(要剛好留下回A地的油),讓對方走掉加的這些油后開始向A地返回,兩者碰頭后一起回A地.那么這個離A地最遠的距離就應該是車行駛一段的距離+停下后給對方的油量可行駛的距離(要留下回A地的油).根據此關系可求出走這個最遠距離所需的油量,然后進行分配即可.
解答: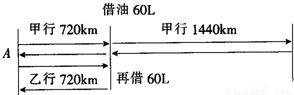
解:設盡可能遠離A地的甲汽車共走了x千米,乙汽車共走了y千米,則
x+y≤240×12×2,且x-y≤240×12
∴x≤4320
所以x最大為4320千米.
設從A到盡可能的離A的距離是m千米,其中借給對方油的那輛車走了n千米后停下,
那么m=n+(240-x÷12×2)×12÷2=1440千米
那么需要用油1440÷12=120升,那么就是走這個最遠距離一次(單趟)需要120升油,
那么可得出的方案是:甲,乙共同走720千米,乙停下等甲,并且給甲60升汽油,甲再走1440千米后回頭與乙會合,乙再給甲60升汽油后,兩車同時回到A地.
也可畫圖表示為:(如右圖).
點評:本題考查一元一次不等式的應用,將現實生活中的事件與數學思想聯系起來,讀懂題列出不等式關系式即可求解.

 解:設盡可能遠離A地的甲汽車共走了x千米,乙汽車共走了y千米,則
解:設盡可能遠離A地的甲汽車共走了x千米,乙汽車共走了y千米,則

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案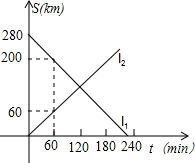 汽車行駛的時間,如圖所示,L1,L2分別表示兩輛汽車的s與t的關系.
汽車行駛的時間,如圖所示,L1,L2分別表示兩輛汽車的s與t的關系.