

 OD×4=
OD×4= ×2t×4=4t;
×2t×4=4t;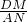 =
=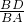 =
=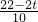 =
=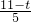 ;
;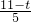 =
= (11-t);
(11-t); S△OBD=
S△OBD= (11-t)=-
(11-t)=- t+
t+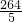 ;
;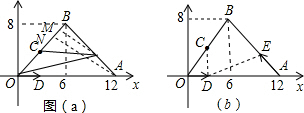
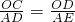 =1,∴OC=AD,即12-2t=5,t=
=1,∴OC=AD,即12-2t=5,t= ;
;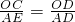 ,即
,即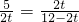 ,解得t=
,解得t=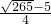 ;
; 或
或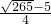 時,兩個三角形相似.
時,兩個三角形相似.

科目:初中數(shù)學(xué) 來源: 題型:
| ||
| 3 |
| ||
| 2 |
 四邊形是平行四邊形.
四邊形是平行四邊形.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,在平面直角坐標(biāo)系中,直y=
如圖,在平面直角坐標(biāo)系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,在平面直角坐標(biāo)系中,O是坐標(biāo)原點,點A的坐標(biāo)是(-2,4),過點A作AB⊥y軸,垂足為B,連接OA.
如圖,在平面直角坐標(biāo)系中,O是坐標(biāo)原點,點A的坐標(biāo)是(-2,4),過點A作AB⊥y軸,垂足為B,連接OA.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
| 3 |

| ||
| 3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 如圖,在平面直角坐標(biāo)系中,原點O處有一乒乓球發(fā)射器向空中發(fā)射乒乓球,乒乓球飛行路線是一條拋物線,在地面上落點落在X軸上為點B.有人在線段OB上點C(靠點B一側(cè))豎直向上擺放無蓋的圓柱形桶,試圖讓乒乓球落入桶內(nèi).已知OB=4米,OC=3米,乒乓球飛行最大高度MN=5米,圓柱形桶的直徑為0.5,高為0.3米(乒乓球的體積和圓柱形桶的厚度忽略不計).
如圖,在平面直角坐標(biāo)系中,原點O處有一乒乓球發(fā)射器向空中發(fā)射乒乓球,乒乓球飛行路線是一條拋物線,在地面上落點落在X軸上為點B.有人在線段OB上點C(靠點B一側(cè))豎直向上擺放無蓋的圓柱形桶,試圖讓乒乓球落入桶內(nèi).已知OB=4米,OC=3米,乒乓球飛行最大高度MN=5米,圓柱形桶的直徑為0.5,高為0.3米(乒乓球的體積和圓柱形桶的厚度忽略不計).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com