【答案】
分析:(1)先把方程整理為一般式,再計算出△=1+4p
2,根據非負數的性質得到△>0,然后根據判別式的意義得這個方程總有兩個不相等的實數根;
(2)根據根與系數的關系得到得x
1+x
2=5,x
1x
2=6-p
2,由已知條件變形得到(x
1+x
2)
2-4x
1x
2=9,即25-4(6-p
2)=9,然后解p的方程即可.
解答:(1)證明:方程整理為x
2-5x+6-p
2=0,
△=(-5)
2-4×1×(6-p
2)
=1+4p
2,
∵4p
2≥0,
∴△>0,
∴這個方程總有兩個不相等的實數根;
(2)根據題意得x
1+x
2=5,x
1x
2=6-p
2,
∵
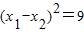
,
∴(x
1+x
2)
2-4x
1x
2=9,即25-4(6-p
2)=9,
∴p=±2
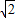
.
點評:本題考查了一元二次方程ax
2+bx+c=0(a≠0)的根的判別式△=b
2-4ac:當△>0,方程有兩個不相等的實數根;當△=0,方程有兩個相等的實數根;當△<0,方程沒有實數根.也考查了一元二次方程的根與系數的關系.

 ,求p的值.
,求p的值.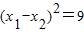 ,
,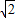 .
.

 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案