
【題目】如圖,邊長為a的菱形ABCD中,∠DAB=60°,E是異于A、D兩點的動點,F是CD上的動點,滿足AE+CF=a,△BEF的周長最小值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
連接BD,可證△ABE≌△DBF,可得BE=BF,可得△BEF為等邊三角形,可得,△BEF的周長為3BE,所以當BE垂直AD時,可求△BEF的周長最小值.
解:連接BD
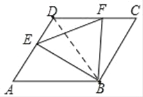
∵ABCD是菱形,∠DAB=60°
∴AB=AD=CD=BC=a,∠C=∠A=60°,∠ADC=∠ABC=120°
∴△ADB,△BDC為等邊三角形,
∴∠ADB=∠ABD=60°=∠BDC=∠DBC,AD=BD=a.
∵AE+CF=a,AE+ED=a,CF+DF=a
∴DF=AE,DE=CF,
∵AE=DF,BD=AB,∠A=∠CDB
∴△AEB≌△DFB
∴BE=BF,∠ABE=∠DBF
∵∠ABE+∠DBE=60°
∴∠DBF+∠DBE=60°即∠EBF=60°
∴△BEF為等邊三角形.
∴△BEF的周長=3BE
根據垂線段最短,即當BE⊥AD時,BE值最小.
在Rt△AEB中,AB=a,∠A=60°
∴AE=![]() a,BE=
a,BE=![]() a
a
∴△BEF的周長最小值是![]() ,
,
故選:B.


科目:初中數學 來源: 題型:
【題目】如圖,等腰△ABC中,AB=AC=![]() ,BC=4,點B在y軸上,BC∥x軸,反比例函數
,BC=4,點B在y軸上,BC∥x軸,反比例函數![]() (x>0)的圖像經過點A,交BC于點D.
(x>0)的圖像經過點A,交BC于點D.
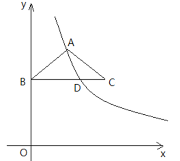
(1)若OB=3,求k的值;
(2)連接CO,若AB=BD,求四邊形ABOC的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】紅紅有兩把不同的鎖和四把不同的鑰匙,其中只有兩把鑰匙能打開對應的兩把鎖,用列表法或樹狀圖求概率.
(1)若取一把鑰匙,求紅紅一次打開鎖的概率;
(2)若取兩把鑰匙,求紅紅恰好打開兩把鎖的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象交x軸于A(﹣2,0),B(1,0),交y軸于C(0,2).
(1)求二次函數的解析式;
(2)連接AC,在直線AC上方的拋物線上是否存在點N,使△NAC的面積最大,若存在,求出這個最大值及此時點N的坐標,若不存在,說明理由;
(3)若點M在x軸上,是否存在點M,使以B、C、M為頂點的三角形是等腰三角形,若存在,直接寫出點M的坐標;若不存在,說明理由;
(4)若P為拋物線上一點,過P作PQ⊥BC于Q,在y軸左側的拋物線是否存在點P使△CPQ∽△BCO(點C與點B對應),若存在,求出點P的坐標,若不存在,說明理由.
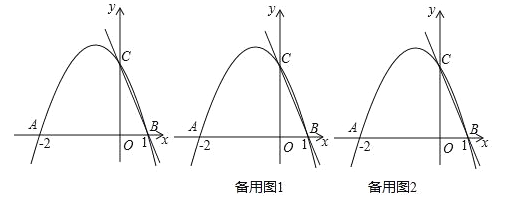
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,格點三角形![]() (頂點為網格線的交點)的頂點
(頂點為網格線的交點)的頂點![]() ,
,![]() 的坐標分別為
的坐標分別為![]() ,
,![]() .
.
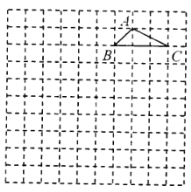
(1)請在網格圖中建立平面直角坐標系;
(2)將![]() 先向左平移5個單位長度,再向下平移6個單位長度,請畫出兩次平移后的
先向左平移5個單位長度,再向下平移6個單位長度,請畫出兩次平移后的![]() ,并直接寫出點
,并直接寫出點![]() 的對應點
的對應點![]() 的坐標;
的坐標;
(3)若![]() 是
是![]() 內一點,直接寫出
內一點,直接寫出![]() 中的對應點
中的對應點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高速發展.阜陽市某家快遞公司,2017年3月份與5月份完成投遞的快遞總件數分別為10萬件和12.1萬件.現假定該公司每月投遞的快遞總件數的增長率相同.
(1)求該快遞公司投遞快遞總件數的月平均增長率?
(2) 如果平均每人每月最多可投遞快遞0.6萬件,那么該公司現有的21名快遞投遞業務員能否完成2017年6月份的快遞投遞任務?如果不能,請問至少需要增加幾名業務員?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】依據國家實行的《國家學生體質健康標準》,對懷柔區初一學生身高進行抽樣調查,以便總結懷柔區初一學生現存的身高問題,分析其影響因素,為學生的健康發展及學校體育教育改革提出合理項建議.已知懷柔區初一學生有男生840人,女生800人,他們的身高在150≤x<175范圍內,隨機抽取初一學生進行抽樣調查.抽取的樣本中,男生比女生多2人,利用所得數據繪制如下統計圖表:

身高情況分組表
組別 | 身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根據統計圖表提供的信息,下列說法中
①抽取男生的樣本中,身高在155≤x<165之間的學生有18人;
②初一學生中女生的身高的中位數在B組;
③抽取的樣本中,抽取女生的樣本容量是38;
④初一學生身高在160≤x<170之間的學生約有800人.
其中合理的是( )
A.①②B.①④C.②④D.③④
查看答案和解析>>
科目:初中數學 來源: 題型:
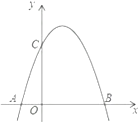
【題目】如圖,是將拋物線y=-x2 平移后得到的拋物線,其對稱軸為x=1,與x軸的一個交點為A(-1,0) ,另一交點為B,與y軸交點為C.
(1)求拋物線的函數表達式;
(2)若點N 為拋物線上一點,且BC⊥NC,求點N的坐標;
(3)點P是拋物線上一點,點Q是一次函數y=![]() x+
x+![]() 的圖象上一點,若四邊形OAPQ為平行四邊形,這樣的點P、Q是否存在?若存在,分別求出點P、Q的坐標,若不存在,說明理由.
的圖象上一點,若四邊形OAPQ為平行四邊形,這樣的點P、Q是否存在?若存在,分別求出點P、Q的坐標,若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com