
某超市經銷一種銷售成本為每件20元的商品.據市場調查分析,如果按每件30元銷售,一周能售出500件,若銷售單價每漲1元,每周的銷售量就減少10件.設銷售單價為每件x元(x≥30),一周的銷售量為y件.
(1)寫出y與x的函數關系式及自變量x的取值范圍;
(2)該超市想通過銷售這種商品一周獲得利潤8000元,銷售單價應定為多少?
科目:初中數學 來源: 題型:解答題
為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔,李明按照相關政策投資銷售本市生產的一種新型節能燈,已知這種節能燈的成本價為每件10元,出廠價為每件12元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=-10x+500.
⑴李明在開始創業的第一個月將銷售單價定為20元,那么政府這個月為他承擔的總差價為多少元?
⑵設李明獲得的利潤為W(元),當銷售單價定為多少元時,每月可獲得最大利潤?
⑶物價部門規定,這種節能燈的銷售單價不得高于25元,如果李明想要每月獲得的利潤不低于3000元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知二次函數y=ax2+bx+3的圖象過點A(-1,0),對稱軸為過點(1,0)且與y軸平行的直線.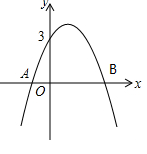
(1)求點B的坐標
(2)求該二次函數的關系式;
(3)結合圖象,解答下列問題:
①當x取什么值時,該函數的圖象在x軸上方?
②當-1<x<2時,求函數y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
在直角坐標平面內,二次函數圖象的頂點為A(1,﹣4),且過點B(3,0).
(1)求該二次函數的解析式;
(2)將該二次函數圖象向右平移幾個單位,可使平移后所得圖象經過坐標原點?并直接寫出平移后所得圖象與x軸的另一個交點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知:拋物線 經過A(
經過A( ,0)、B(5,0)兩點,頂點為P.
,0)、B(5,0)兩點,頂點為P.
求:(1)求b,c的值;
(2)求△ABP的面積;
(3)若點C( ,
, )和點D(
)和點D( ,
, )在該拋物線上,則當
)在該拋物線上,則當 時,
時,
請寫出 與
與 的大小關系.
的大小關系.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
某個體戶春節前代理銷售某種品牌的酒,已知進價為每件40元,生產廠家要求銷售價不少于40元,且不大于70元,市場調查發現:若每件以50元銷售,平均每天可銷售90件,價格每降低1元,平均每天多銷售3件,價格每升高1元,平均每天少銷售3件.
(1)寫出平均每天銷售量y(件)與每件銷售價x(元)之間的函數關系式,并注明自變量的取值范圍;
(2)求出該個體戶每天銷售這種酒的毛利潤W(元)與每件酒的售價x(元)之間的函數關系式,并注明自變量的取值范圍(每件的毛利潤=售價-進價);
(3)當酒的售價為多少時平均每天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,已知拋物線y=ax2+bx+c(a≠0)的頂點坐標為(4,﹣ ),且與y軸交于點C(0,2),與x軸交于A,B兩點(點A在點B的左邊).
),且與y軸交于點C(0,2),與x軸交于A,B兩點(點A在點B的左邊).
(1)求拋物線的解析式及A、B兩點的坐標;
(2)在(1)中拋物線的對稱軸l上是否存在一點P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,請說明理由;
(3)以AB為直徑的⊙M相切于點E,CE交x軸于點D,求直線CE的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知拋物線與x軸相交于兩點A(1,0),B(-3,0),與y軸相交于點C(0,3).
(1)求此拋物線的函數表達式;
(2)如果點 是拋物線上的一點,求△ABD的面積.
是拋物線上的一點,求△ABD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
高盛超市準備進一批季節性小家電,每個進價為40元,經市場預測,銷售定價為50元,可售出400個;定價每增加1元,銷售量將減少10個.
(1)設每個小家電定價增加 元,每售出一個小家電可獲得的利潤是多少元?(用含
元,每售出一個小家電可獲得的利潤是多少元?(用含 的代數式表示)
的代數式表示)
(2)當定價增加多少元時,商店獲得利潤6000元 ?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com