
【題目】對于一個矩形ABCD及⊙M給出如下定義:在同一平面內,如果矩形ABCD的四個頂點到⊙M上一點的距離相等,那么稱這個矩形ABCD是⊙M的“伴侶矩形”.如圖,在平面直角坐標系xOy中,直線l:y= ![]() x﹣3交x軸于點M,⊙M的半徑為2,矩形ABCD沿直線運動(BD在直線l上),BD=2,AB∥y軸,當矩形ABCD是⊙M的“伴侶矩形”時,點C的坐標為 .
x﹣3交x軸于點M,⊙M的半徑為2,矩形ABCD沿直線運動(BD在直線l上),BD=2,AB∥y軸,當矩形ABCD是⊙M的“伴侶矩形”時,點C的坐標為 . 
【答案】( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() +
+ ![]() ,
, ![]() )
)
【解析】解:如圖所示,矩形在這兩個位置時就是⊙M的“伴侶矩形”,根據直線l:y= ![]() x﹣3得:OM=
x﹣3得:OM= ![]() ,ON=3,由勾股定理得:MN=
,ON=3,由勾股定理得:MN= ![]() =2
=2 ![]() ,
,
①矩形在x軸下方時,分別過A、D作兩軸的垂線AH、DG,
由cos∠ABD=cos∠ONM= ![]() ,∴
,∴ ![]() =
= ![]() ,AB=
,AB= ![]() ,則AD=1,
,則AD=1,
∵DG∥y軸,
∴△MDG∽△MON,
∴ ![]() ,∴
,∴ ![]() ,∴DG=
,∴DG= ![]() ,∴CG=
,∴CG= ![]() +
+ ![]() =
= ![]() ,同理可得:
,同理可得: ![]() ,∴
,∴ ![]() ,∴DH=
,∴DH= ![]() ,∴C(
,∴C( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() );②矩形在x軸上方時,同理可得:C(
);②矩形在x軸上方時,同理可得:C( ![]()
![]() ,
, ![]() );
);
故答案為:( ![]() ﹣
﹣ ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() +
+ ![]() ,
, ![]() ).
).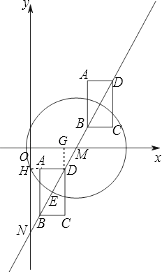
根據“伴侶矩形”的定義可知:圓上的點一定在矩形的對角線交點上,因為只有對角線交點到四個頂點的距離相等,由此畫出圖形,先求出直線與x軸和y軸兩交點的坐標,和矩形的長和寬;
有兩種情況:①矩形在x軸下方時,作輔助線構建相似三角形得比例式,分別求出DG和DH的長,從而求出CG的長,根據坐標特點寫出點C的坐標;②矩形在x軸上方時,也分別過C、B兩點向兩坐標軸作垂線,利用平行相似得比例式,求出:C( ![]()
![]() ,
, ![]() ).此題主要考查了圓的綜合應用以及相似三角形的性質和矩形等知識,綜合性較強,解答本題需要我們熟練各部分的內容,對學生的綜合能力要求較高,一定要注意將所學知識貫穿起來.同時,正確理解題意準確畫出符合條件的矩形是本題的關鍵,這就需要熟練掌握矩形的對角線的交點到四個頂點的距離相等.
).此題主要考查了圓的綜合應用以及相似三角形的性質和矩形等知識,綜合性較強,解答本題需要我們熟練各部分的內容,對學生的綜合能力要求較高,一定要注意將所學知識貫穿起來.同時,正確理解題意準確畫出符合條件的矩形是本題的關鍵,這就需要熟練掌握矩形的對角線的交點到四個頂點的距離相等.


 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:初中數學 來源: 題型:
【題目】如圖,將矩形紙片ABCD(AD>AB)折疊,使點C剛好落在線段AD上,且折痕分別與邊BC,AD相交,設折疊后點C,D的對應點分別為點G,H,折痕分別與邊BC,AD相交于點E,F.
(1)判斷四邊形CEGF的形狀,并證明你的結論;
(2)若AB=3,BC=9,求線段CE的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】利用數軸解決問題:我們知道,若數軸上點![]() 表示的數是
表示的數是![]() ,點
,點![]() 表示的數是
表示的數是![]() ,則
,則![]() 、
、![]() 兩點間的距離記作
兩點間的距離記作![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,則
,則![]() = ;
= ;
(2)若數軸上一點![]() 表示的數是
表示的數是![]() ,
,![]() ,則
,則![]() = ;
= ;
(3)若點![]() 表示的數是
表示的數是![]() ,已知
,已知![]() ,點
,點![]() 在
在![]() 的左邊,
的左邊,![]() ,點
,點![]() 在點
在點![]() 的右邊,
的右邊,![]() ,點
,點![]() 以每秒
以每秒![]() 的速度向右移動,同時點
的速度向右移動,同時點![]() 、點
、點![]() 分別以每秒
分別以每秒![]() 、
、![]() 的速度向左移動.設移動時間為
的速度向左移動.設移動時間為![]() 秒,那么
秒,那么![]() 是否有最小值?若有,求出最小值并寫出此時
是否有最小值?若有,求出最小值并寫出此時![]() 的取值范圍;若沒有,請說明理由.
的取值范圍;若沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c經過A(﹣1,0),B(3,0)兩點,且與y軸交于點C,點D是拋物線的頂點,拋物線的對稱軸DE交x軸于點E,連接BD.
(1)求經過A,B,C三點的拋物線的函數表達式;
(2)點P是線段BD上一點,當PE=PC時,求點P的坐標;
(3)在(2)的條件下,過點P作PF⊥x軸于點F,G為拋物線上一動點,M為x軸上一動點,N為直線PF上一動點,當以F、M、G為頂點的四邊形是正方形時,請求出點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c的圖象如圖所示,對稱軸是直線x=﹣1,有以下結論:①abc>0;②4ac<b2;③2a+b=0;④a﹣b+c>2.其中正確的結論的個數是( ) 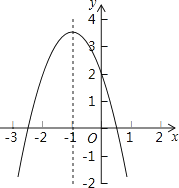
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一垂直于地面的燈柱AB被一鋼筋CD固定,CD與地面成45°夾角(∠CDB=45°),在C點上方2米處加固另一條鋼線ED,ED與地面成53°夾角(∠EDB=53°),那么鋼線ED的長度約為多少米?(結果精確到1米,參考數據:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)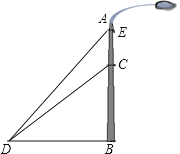
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.則下列結論: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正確結論__________(填編號).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正確結論__________(填編號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB與CD相交于點O,OD平分∠BOE,OF⊥OD。
(1)∠AOF與∠EOF相等嗎?
(2)寫出圖中和∠DOE互補的角。
(3)若∠BOE=600,求∠AOD和∠EOF的度數。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AC與BD相交于點O,E為OD的中點,連接AE并延長交DC于點F,則S△DEF:S△AOB的值為( ) 
A.1:3
B.1:5
C.1:6
D.1:11
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com