
【題目】如圖,已知直線y=k1x+b與x軸,y軸相交于P,Q兩點,則y= ![]() 的圖象相交于A(﹣2,m),B(1,n)兩點,連接OA,OB,給出下列結論:①k1k2<0;②m+
的圖象相交于A(﹣2,m),B(1,n)兩點,連接OA,OB,給出下列結論:①k1k2<0;②m+ ![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b> ![]() 的解集在x<﹣2或0<x<1,其中正確的結論是( )
的解集在x<﹣2或0<x<1,其中正確的結論是( ) 
A.②③④
B.①②③④
C.③④
D.②③
科目:初中數學 來源: 題型:
【題目】如圖,O為直線AB上一點,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)請你數一數,圖中有多少個小于平角的角;
(2)求出∠BOD的度數;
(3)請通過計算說明OE是否平分∠BOC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l:y=﹣3x+3與x軸、y軸分別相交于A、B兩點,拋物線y=ax2﹣2ax+a+4(a<0)經過點B.
(1)求該拋物線的函數表達式;
(2)已知點M是拋物線上的一個動點,并且點M在第一象限內,連接AM、BM,設點M的橫坐標為m,△ABM的面積為S,求S與m的函數表達式,并求出S的最大值;
(3)在(2)的條件下,當S取得最大值時,動點M相應的位置記為點M′.
①寫出點M′的坐標;
②將直線l繞點A按順時針方向旋轉得到直線l′,當直線l′與直線AM′重合時停止旋轉,在旋轉過程中,直線l′與線段BM′交于點C,設點B、M′到直線l′的距離分別為d1、d2 , 當d1+d2最大時,求直線l′旋轉的角度(即∠BAC的度數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖數軸上A、B、C三點對應的數分別是a、b、7,滿足OA=3,BC=1,P為數軸上一動點,點P從A出發,沿數軸正方向以每秒1.5個單位長度的速度勻速運動,點Q從點C出發在射線CA上向點A勻速運動,且P、Q兩點同時出發.
(1)求a、b的值
(2)當P運動到線段OB的中點時,點Q運動的位置恰好是線段AB靠近點B的三等分點,求點Q的運動速度
(3)當P、Q兩點間的距離是6個單位長度時,求OP的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在長方形![]() 中,AB=4cm,BC=6cm,點
中,AB=4cm,BC=6cm,點![]() 為
為![]() 中點,如果點
中點,如果點![]() 在線段
在線段![]() 上以每秒2cm的速度由點
上以每秒2cm的速度由點![]() 向點
向點![]() 運動,同時,點
運動,同時,點![]() 在線段
在線段![]() 上由點
上由點![]() 向點
向點![]() 運動.設點
運動.設點![]() 運動時間為
運動時間為![]() 秒,若某一時刻△BPE與△CQP全等,求此時
秒,若某一時刻△BPE與△CQP全等,求此時![]() 的值及點
的值及點![]() 的運動速度.
的運動速度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD為BC邊上的高.動點P從點A出發,沿A→D方向以 ![]() cm/s的速度向點D運動.設△ABP的面積為S1 , 矩形PDFE的面積為S2 , 運動時間為t秒(0<t<8),則t=秒時,S1=2S2 .
cm/s的速度向點D運動.設△ABP的面積為S1 , 矩形PDFE的面積為S2 , 運動時間為t秒(0<t<8),則t=秒時,S1=2S2 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】.. 計算題:
(1)8﹣(﹣10)﹣|﹣2|
(2)2 ![]() ﹣3
﹣3![]() +(﹣3
+(﹣3![]() )﹣(+5
)﹣(+5![]() )
)
(3)﹣24×(﹣ ![]() +
+![]() ﹣
﹣![]() )
)
(4)﹣49 ![]() ×10(簡便運算)
×10(簡便運算)
(5)﹣ ![]() ÷(
÷(![]() ﹣
﹣![]() +
+![]() )
)
(6)3×(﹣38 ![]() )﹣4×(﹣38
)﹣4×(﹣38 ![]() )﹣38
)﹣38![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,AB∥CD,點P為定點,E、F分別是AB、CD上的動點.
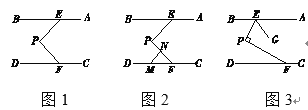
(1)求證:∠P=∠BEP+∠PFD;
(2)若點M為CD上一點,如圖2,∠FMN=∠BEP,且MN交PF于N.試說明∠EPF與∠PNM的數量關系,并證明你的結論;
(3)移動E、F使得∠EPF=90°,如圖3,作∠PEG=∠BEP,求∠AEG與∠PFD度數的比值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB=CB,BE=BF,點A,B,C在同一條直線上,∠1=∠2.
(1)證明:△ABE≌△CBF;
(2)若∠FBE=40°,∠C=45°,求∠E的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com