
【題目】端午節期間,某校“慈善小組”籌集到1240元善款,全部用于購買水果和粽子,然后到福利院送給老人,決定購買大棗粽子和普通粽子共20盒,剩下的錢用于購買水果,要求購買水果的錢數不少于180元但不超過240元.已知大棗粽子比普通粽子每盒貴15元,若用300元恰好可以買到2盒大棗粽子和4盒普通粽子.
(1)請求出兩種口味的粽子每盒的價格;
(2)設買大棗粽子x盒,買水果共用了w元. ①請求出w關于x的函數關系式;
②求出購買兩種粽子的可能方案,并說明哪一種方案使購買水果的錢數最多.
【答案】
(1)解:設買大棗粽子x元/盒,普通粽子y元/盒,
根據題意得, ![]() ,
,
解得 ![]() .
.
答:大棗粽子60元/盒,普通粽子45元/盒
(2)解:①設買大棗粽子x盒,則購買普通粽子(20﹣x)盒,買水果共用了w元,
根據題意得,w=1240﹣60x﹣45(20﹣x),
=1240﹣60x﹣900+45x,
=﹣15x+340,
故,w關于x的函數關系式為w=﹣15x+340;
②∵要求購買水果的錢數不少于180元但不超過240元,
∴ 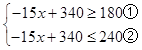 ,
,
解不等式①得,x≤10 ![]() ,
,
解不等式②得,x≥6 ![]() ,
,
所以,不等式組的解集是6 ![]() ≤x≤10
≤x≤10 ![]() ,
,
∵x是正整數,
∴x=7、8、9、10,
可能方案有:
方案一:購買大棗粽子7盒,普通粽子13盒,
方案二:購買大棗粽子8盒,普通粽子12盒,
方案三:購買大棗粽子9盒,普通粽子11盒,
方案四:購買大棗粽子10盒,普通粽子10盒;
∵﹣15<0,
∴w隨x的增大而減小,
∴方案一可使購買水果的錢數最多,最多為﹣15×7+340=235元
【解析】(1)設買大棗粽子x元/盒,普通粽子y元/盒,根據兩種粽子的單價和購買兩種粽子用300元列出二元一次方程組,然后求解即可;(2)①表示出購買普通粽子的(20﹣x)盒,然后根據購買水果的錢數等于善款總數減去購買兩種粽子的錢數,整理即可得解;②根據購買水果的錢數不少于180元但不超過240元列出不等式組,然后求解得到x的取值范圍,再根據粽子的盒數是正整數從而寫出所有的可能購買方案,再根據一次函數的增減性求出購買水果錢數最多的方案.


科目:初中數學 來源: 題型:
【題目】將n張長度為10 cm的紙條,一張接一張地黏成一張長紙條,黏合部分的長度都是3 cm,則這張黏合后的長紙條總長是cm(用含n的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】工人師傅砌門時,常用一根木條固定長方形門框,使其不變形,這樣做的根據( )
A. 兩點之間的線段最短 B. 三角形具有穩定性
C. 長方形是軸對稱圖形 D. 長方形的四個角都是直角
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜邊AC,交AB于D,E是垂足,連接CD.若BD=1,則AC的長是( ) 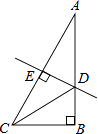
A.2 ![]()
B.2
C.4 ![]()
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】蠶絲是最細的天然纖維,它的截面直徑約為0.000001米,這一數據用科學記數法表示為( )
A.1×106米
B.1×10﹣5米
C.1×10﹣6米
D.1×105米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是邊長為1的正方形,點E在AD邊上運動,且不與點A和點D重合,連結CE,過點C作CF⊥CE交AB的延長線于點F,EF交BC于點G.
(1)求證:△CDE≌△CBF;
(2)當DE=![]() 時,求CG的長;
時,求CG的長;
(3)連結AG,在點E運動過程中,四邊形CEAG能否為平行四邊形?若能,求出此時DE的長;若不能,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O(0,0),A(0,1)是正方形OAA1B的兩個頂點,以OA1對角線為邊作正方形OA1A2B1 , 再以正方形的對角線OA2作正方形OA1A2B1 , …,依此規律,則點A8的坐標是( )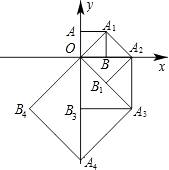
A.(﹣8,0)
B.(0,8)
C.(0,8 ![]() )
)
D.(0,16)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com