
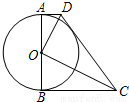
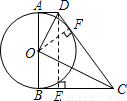
 解:(1)①S△COD=S梯形ABCD-S△AOD-S△BOC
解:(1)①S△COD=S梯形ABCD-S△AOD-S△BOC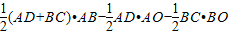
 =40-4-16=20.
=40-4-16=20.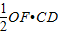 =20,可得OF=4,
=20,可得OF=4,
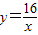 ,x>0.
,x>0.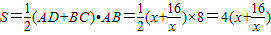 ,x>0.
,x>0.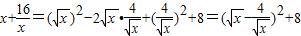 ,
,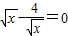 ,x=4時,
,x=4時,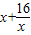 有最小值8,從而S有最小值32.
有最小值8,從而S有最小值32.

 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:初中數學 來源: 題型:
 如圖,四邊形ABCD的對角線AC與BD互相垂直平分于點O,設AC=2a,BD=2b,請推導這個四邊形的性質.(至少3條)
如圖,四邊形ABCD的對角線AC與BD互相垂直平分于點O,設AC=2a,BD=2b,請推導這個四邊形的性質.(至少3條)查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,四邊形ABCD的對角線AC、BD交于點P,過點P作直線交AD于點E,交BC于點F.若PE=PF,且AP+AE=CP+CF.
如圖,四邊形ABCD的對角線AC、BD交于點P,過點P作直線交AD于點E,交BC于點F.若PE=PF,且AP+AE=CP+CF.查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com