
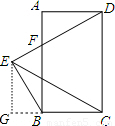
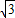 ,△DCE是等邊三角形,DE交AB于點(diǎn)F,求△BEF的周長(zhǎng).
,△DCE是等邊三角形,DE交AB于點(diǎn)F,求△BEF的周長(zhǎng).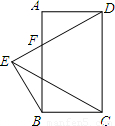
 ,
,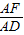 ,
,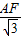 =
=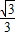 ,
,
 EC=
EC= ,cos∠ECG=
,cos∠ECG=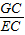 ,
,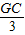 =
= ,
,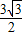 ,
, -
-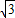 =
= ,
, (舍去負(fù)值);
(舍去負(fù)值);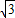 .
.
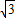 ,
, ,
, =
=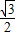 ,
,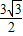 ,
,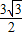 -
- =
=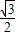 .
.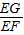 ,
,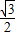 =
=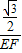 ,
, EF=
EF= ,
, AB=
AB= ,
,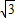 (舍去負(fù)值),
(舍去負(fù)值),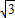 .
.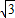 ,
,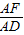 ,
,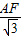 =
=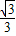 ,
,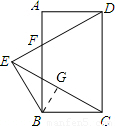
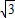 ,∠ECB=30°,
,∠ECB=30°, BC=
BC=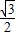 ,cos∠BCG=
,cos∠BCG=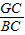 ,
, =
=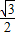 ,
, ,
, =
= ,
,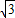 (舍去負(fù)值)或BE=BC,
(舍去負(fù)值)或BE=BC,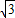 .
.

 通城學(xué)典默寫能手系列答案
通城學(xué)典默寫能手系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 如圖,在矩形ABCD中,AB=4cm,BC=8cm,點(diǎn)P從點(diǎn)A出發(fā)以1cm/s的速度向點(diǎn)B運(yùn)動(dòng),點(diǎn)Q從點(diǎn)B出發(fā)以2cm/s的速度向點(diǎn)C運(yùn)動(dòng),設(shè)經(jīng)過(guò)的時(shí)間為xs,△PBQ的面積為ycm2,則下列圖象能反映y與x之間的函數(shù)關(guān)系的是( )
如圖,在矩形ABCD中,AB=4cm,BC=8cm,點(diǎn)P從點(diǎn)A出發(fā)以1cm/s的速度向點(diǎn)B運(yùn)動(dòng),點(diǎn)Q從點(diǎn)B出發(fā)以2cm/s的速度向點(diǎn)C運(yùn)動(dòng),設(shè)經(jīng)過(guò)的時(shí)間為xs,△PBQ的面積為ycm2,則下列圖象能反映y與x之間的函數(shù)關(guān)系的是( )A、 | B、 | C、 | D、 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 .
.| 2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 動(dòng)過(guò)程中,Q點(diǎn)停留了1s,圖②是P、Q兩點(diǎn)在折線AB-BC-CD上相距的路程S(cm)與時(shí)間t(s)之間的函數(shù)關(guān)系圖象.
動(dòng)過(guò)程中,Q點(diǎn)停留了1s,圖②是P、Q兩點(diǎn)在折線AB-BC-CD上相距的路程S(cm)與時(shí)間t(s)之間的函數(shù)關(guān)系圖象.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 DE,EF與AB交于點(diǎn)F,設(shè)CE=x,BF=y.
DE,EF與AB交于點(diǎn)F,設(shè)CE=x,BF=y.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com