
【題目】一位同學拿了兩塊45°的三角尺△MNK,△ACB做了一個探究活動:將△MNK的直角頂點M放在△ABC的斜邊AB的中點處,設AC=BC=a.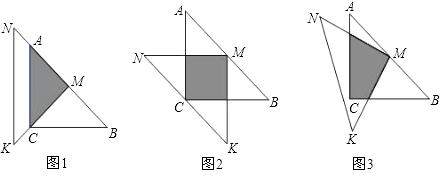
(1)如圖1,兩個三角尺的重疊部分為△ACM,則重疊部分的面積為 , 周長為;
(2)將圖1中的△MNK繞頂點M逆時針旋轉45°,得到圖2,此時重疊部分的面積為 , 周長為;
(3)如果將△MNK繞M旋轉到不同于圖1,圖2的位置,如圖3所示,猜想此時重疊部分的面積為多少?并試著加以驗證.
【答案】
(1)![]() ;(1+
;(1+ ![]() )a
)a
(2)![]() a2
a2![]() ;2a
;2a
(3)
解:猜想:重疊部分的面積為 ![]() .
.
理由如下:
過點M分別作AC、BC的垂線MH、MG,垂足為H、G
設MN與AC的交點為E,MK與BC的交點為F
∵M是△ABC斜邊AB的中點,AC=BC=a
∴MH=MG= ![]()
又∵∠HME+∠HMF=∠GMF+∠HMF,
∴∠HME=∠GMF,
∴Rt△MHE≌Rt△MGF
∴陰影部分的面積等于正方形CGMH的面積
∵正方形CGMH的面積是MGMH= ![]() ×
× ![]() =
= ![]()
∴陰影部分的面積是 ![]() .
.

【解析】解:(1)∵AM=MC= ![]() AC=
AC= ![]() a,則
a,則
∴重疊部分的面積是△ACB的面積的一半為 ![]() a2 , 周長為(1+
a2 , 周長為(1+ ![]() )a.(2)∵重疊部分是正方形
)a.(2)∵重疊部分是正方形
∴邊長為 ![]() a,面積為
a,面積為 ![]() a2 , 周長為2a.
a2 , 周長為2a.
(1)由等腰直角三角形的性質:底邊上的中線與底邊上的高重合,得到△AMC是等腰直角三角形,AM=MC= ![]() AC=
AC= ![]() a,則重疊部分的面積是△ACB的面積的一半,為
a,則重疊部分的面積是△ACB的面積的一半,為 ![]() a2 , 周長為(1+
a2 , 周長為(1+ ![]() )a.(2)易得重疊部分是正方形,邊長為
)a.(2)易得重疊部分是正方形,邊長為 ![]() a,面積為
a,面積為 ![]() a2 , 周長為2a.(3)過點M分別作AC、BC的垂線MH、MG,垂足為H、G.求得Rt△MHE≌Rt△MGF,則陰影部分的面積等于正方形CGMH的面積.
a2 , 周長為2a.(3)過點M分別作AC、BC的垂線MH、MG,垂足為H、G.求得Rt△MHE≌Rt△MGF,則陰影部分的面積等于正方形CGMH的面積.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC邊在直線a上,將△ABC繞點A順時針旋轉到位置①可得到點P1 , 此時AP1= ![]() ;將位置①的三角形繞點P1順時針旋轉到位置②可得到點P2 , 此時AP2=
;將位置①的三角形繞點P1順時針旋轉到位置②可得到點P2 , 此時AP2= ![]() +1;將位置②的三角形繞點P2順時針旋轉到位置③可得到點P3時,AP3=
+1;將位置②的三角形繞點P2順時針旋轉到位置③可得到點P3時,AP3= ![]() +2…按此規律繼續旋轉,直至得到點P2026為止,則AP2016= .
+2…按此規律繼續旋轉,直至得到點P2026為止,則AP2016= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個半圓形橋洞截面示意圖,圓心為O,直徑AB是河底線,弦CD是水位線,CD∥AB,且AB=26m,OE⊥CD于點E.水位正常時測得OE:CD=5:24
(1)求CD的長;
(2)現汛期來臨,水面要以每小時4m的速度上升,則經過多長時間橋洞會剛剛被灌滿?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,對角線BD的垂直平分線MN與AD相交于點M,與BC相交于點N,連接BM,DN. 
(1)求證:四邊形BMDN是菱形;
(2)若AB=4,AD=8,求MD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在Rt△ABC中,∠C=90°,BC=6cm,AC=8 cm,AB=10 cm. 現有一動點P,從A點出發,沿著三角形的邊AC-CB-BA運動,回到A點停止,速度為1 cm/s,設運動時間為t s.
(1)當t=_______時,△ABC的周長被線段AP平分為相等的兩部分.
(2)當t=_______時,△APC的面積等于△ABC面積的一半.
(3)還有一個△DEF,∠E=90°,如圖②所示,DE=4cm,DF=5cm,∠D=∠A. 在△ABC的邊上,若另外有一個動點Q,與P 同時從A點出發,沿著邊AB-BC-CA運動,回到點A停止. 在兩點運動過程中某一時刻,恰好△APQ與△DEF全等,則點Q的運動速度 cm/s.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將等邊△ABC繞點C順時針旋轉120°得到△EDC,連接AD,BD.則下列結論:
①AC=AD;②BD⊥AC;③四邊形ACED是菱形.
其中正確的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某市近郊有一塊長為60米,寬為50米的矩形荒地,地方政府準備在此建一個綜合性休閑廣場,其中陰影部分為通道,通道的寬度均相等,中間的三個矩形(其中三個矩形的一邊長均為a米)區域將鋪設塑膠地面作為運動場地. 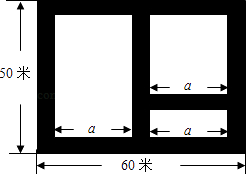
(1)設通道的寬度為x米,則a=(用含x的代數式表示);
(2)若塑膠運動場地總占地面積為2430平方米.請問通道的寬度為多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P是正三角形ABC內的一點,且PA=5,PB=12,PC=13,若將△PAC繞點A逆時針旋轉后,得到△P′AB,求點P與點P′之間的距離及∠APB的度數. 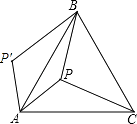
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC為等邊三角形,點D、E分別在BC、AC邊上,AD與BE相交于點F,且AE=CD.
(1)求證:AD=BE;
(2)求∠BFD的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com