
【題目】如圖,直線l切⊙O于點A,點P為直線l上一點,直線PO交⊙O于點C、B,點D在線段AP上,連接DB,且AD=DB.
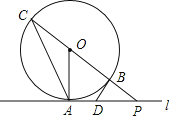
(1)求證:DB為⊙O的切線;(2)若AD=1,PB=BO,求弦AC的長.
【答案】(1)見解析;(2)AC=3.
【解析】
(1)要證明DB為⊙O的切線,只要證明∠OBD=90即可.
(2)根據已知及直角三角形的性質可以得到PD=2BD=2DA=2,再利用等角對等邊可以得到AC=AP,這樣求得AP的值就得出了AC的長.
(1)證明:連接OD;
∵PA為⊙O切線,
∴∠OAD=90°;
在△OAD和△OBD中,
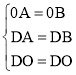 ,
,
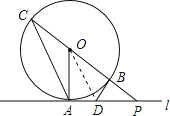
∴△OAD≌△OBD,
∴∠OBD=∠OAD=90°,
∴OB⊥BD
∴DB為⊙O的切線
(2)解:在Rt△OAP中;
∵PB=OB=OA,
∴OP=2OA,
∴∠OPA=30°,
∴∠POA=60°=2∠C,
∴PD=2BD=2DA=2,
∴∠OPA=∠C=30°,
∴AC=AP=3.


科目:初中數學 來源: 題型:
【題目】為迎接2011年高中招生考試,某中學對全校九年級學生進行了一次數學摸底考試,并隨機抽取了部分學生的測試成績作為樣本進行,繪制成了如下兩幅不完整的統計圖,請根據圖中所給信息,下列問題:
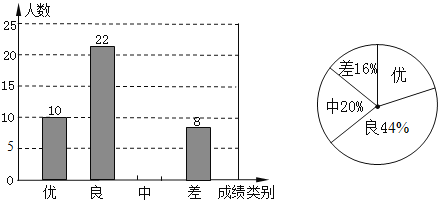
(1)請將表示成績類別為“中”的條形統計圖補充完整;
(2)在扇形統計圖中,表示成績類別為“優”的扇形所對應的圓心角是 72 度;
(3)學校九年級共有1000人參加了這次數學考試,估算該校九年級共有多少名學生的數學成績可以達到優秀?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】自2017年3月起,成都市中心城區居民用水實行以戶為單位的三級階梯收費辦法:
第I級:居民每戶每月用水18噸以內含18噸每噸收水費a元;
第Ⅱ級:居民每戶每月用水超過18噸但不超過25噸,未超過18噸的部分按照第Ⅰ級標準收費,超過部分每噸收水費b元;
第Ⅲ級:居民每戶每月用水超過25噸,未超過25噸的部分按照第I、Ⅱ級標準收費,超過部分每噸收水費c元.
設一戶居民月用水x噸,應繳水費為y元,y與x之間的函數關系如圖所示
(1)根據圖象直接作答:a= ,b= ;
(2)求當x≥25時y與x之間的函數關系;
(3)把上述水費階梯收費辦法稱為方案①,假設還存在方案②:居民每戶月用水一律按照每噸4元的標準繳費,請你根據居民每戶月“用水量的大小設計出對居民繳費最實惠的方案.(寫出過程)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圓規作∠ABC的平分線BD交AC于點D(保留作圖痕跡,不要求寫作法);
(2)在(1)中作出∠ABC的平分線BD后,求∠BDC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,OA=AB,∠OAB=90°,反比例函數y=![]() (x>0)的圖象經過A,B兩點.若點A的坐標為(n,1),則 k的值為______.
(x>0)的圖象經過A,B兩點.若點A的坐標為(n,1),則 k的值為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
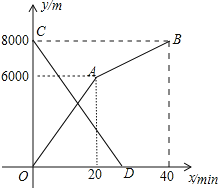
【題目】小明和小亮分別從甲地和乙地同時出發,沿同一條路相向而行,小明開始跑步,中途改為步行,到達乙地恰好用![]() 小亮騎自行車以
小亮騎自行車以![]() 的速度直接到甲地,兩人離甲地的路程
的速度直接到甲地,兩人離甲地的路程![]() 與各自離開出發地的時間
與各自離開出發地的時間![]() 之間的函數圖象如圖所示,
之間的函數圖象如圖所示,
![]() 甲、乙兩地之間的路程為______m,小明步行的速度為______
甲、乙兩地之間的路程為______m,小明步行的速度為______![]() ;
;
![]() 求小亮離甲地的路程y關于x的函數表達式,并寫出自變量x的取值范圍;
求小亮離甲地的路程y關于x的函數表達式,并寫出自變量x的取值范圍;
![]() 求兩人相遇的時間.
求兩人相遇的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線![]() 經過點A,作AB⊥x軸于點B,將△ABO繞點B逆時針旋轉60°得到△CBD.若點B的坐標為(2, 0),則點C的坐標為( )
經過點A,作AB⊥x軸于點B,將△ABO繞點B逆時針旋轉60°得到△CBD.若點B的坐標為(2, 0),則點C的坐標為( )

A.(﹣1,![]() )B.(﹣2,
)B.(﹣2,![]() )C.(
)C.(![]() ,1)D.(
,1)D.(![]() ,2)
,2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com