
 如圖1,等腰直角△ABC的頂點A,B的坐標分別為(0,10),(8,4),頂點C在第一象限.點P從點A出發,沿△ABC的邊按逆時針方向勻速運動,同時,點O從點E(4,0)出發,沿x軸正方向以相同速度運動.當點P到達點C時.P、Q兩點同時停止運動,設運動的時間為t秒,
如圖1,等腰直角△ABC的頂點A,B的坐標分別為(0,10),(8,4),頂點C在第一象限.點P從點A出發,沿△ABC的邊按逆時針方向勻速運動,同時,點O從點E(4,0)出發,沿x軸正方向以相同速度運動.當點P到達點C時.P、Q兩點同時停止運動,設運動的時間為t秒,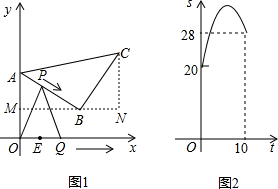
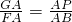 ,
, t,
t, t,
t, OQ×OG=
OQ×OG= (4+t)( 10-
(4+t)( 10- t)
t)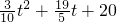
 (t2-
(t2- t)+20
t)+20 (t-
(t- )2+
)2+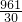
 時,S有最大值,此時,GP=
時,S有最大值,此時,GP=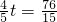 ,OG=10-
,OG=10- t=
t=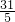
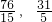 )
)  OQ=
OQ=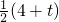 .
.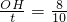 ,OH=
,OH=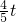
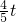 =
=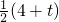 ,t=
,t=
 OQ=
OQ=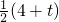 ,PB=t-10,BA=10,AF=6,
,PB=t-10,BA=10,AF=6,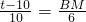 ,BM=
,BM= (t-10),
(t-10), (t-10)=
(t-10)=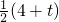 ,t=0(舍去),
,t=0(舍去), 時,OP=PQ
時,OP=PQ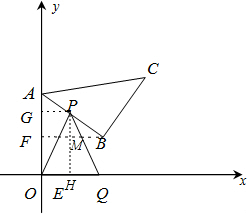


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 目標測試系列答案
目標測試系列答案科目:初中數學 來源: 題型:
 如圖,在等腰直角△ABC中,∠B=90°,將△ABC繞頂點A逆時針方向旋轉60°后得到△AB′C′,則∠BAC′=( )
如圖,在等腰直角△ABC中,∠B=90°,將△ABC繞頂點A逆時針方向旋轉60°后得到△AB′C′,則∠BAC′=( )查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖△ABC是等腰直角三角形,BC是斜邊,將△ABP繞點A逆時針旋轉后,能與△ACP′重合,已知AP=3,則PP′的長度是( )
如圖△ABC是等腰直角三角形,BC是斜邊,將△ABP繞點A逆時針旋轉后,能與△ACP′重合,已知AP=3,則PP′的長度是( )
|
|
查看答案和解析>>
科目:初中數學 來源: 題型:
| 6 |

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com