已知一組數據x1,x2,…,xn的方差是a,則數據x1-4,x2-4,…,xn-4的方差是 ;數據 3x1,3x2,…,3xn的方差是 .
【答案】
分析:首先設原數據的平均數為
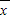
,則新數據的平均數為
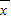
-4和3
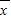
,然后利用方差的公式計算即可得到答案.
解答:解:由題意知,原數據的平均數為
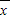
,新數據的每一個數都減去了4,則平均數變為
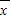
-4,
∵S
12=
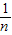
[(x
1-
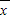
)
2+(x
2-
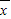
)
2+…+(x
n-

)
2]=a,
∴S
22=

[(x
1-4-

-4)
2+(x
2-4-
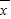
-4)
2+…+(x
n-4-

-4)
2]
=
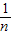
[(x
1-
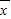
)
2+(x
2-
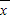
)
2+…+(x
n-
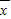
)
2]=a,
所以方差不變.
原數據的平均數為
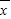
,新數據的每一個數都乘以了3,則平均數變為3
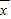
,
∵S
12=
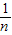
[(x
1-

)
2+(x
2-
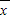
)
2+…+(x
n-
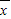
)
2]=a,
∴S
22=
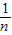
[(3x
1-3
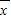
)
2+(3x
2-3
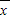
)
2+…+(3x
n-3
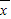
)
2]
=9×
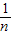
[(x
1-
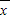
)
2+(x
2-
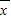
)
2+…+(x
n-
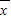
)
2]
=9a,
故答案為:a,9a.
點評:本題考查了方差的定義.當數據都加上一個數(或減去一個數)時,平均數也加或減這個數,方差不變,即數據的波動情況不變;當數據都乘以一個數(或除以一個數)時,平均數也乘以或除以這個數,方差變為這個數的平方倍.

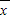 ,則新數據的平均數為
,則新數據的平均數為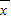 -4和3
-4和3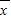 ,然后利用方差的公式計算即可得到答案.
,然后利用方差的公式計算即可得到答案.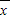 ,新數據的每一個數都減去了4,則平均數變為
,新數據的每一個數都減去了4,則平均數變為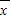 -4,
-4,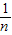 [(x1-
[(x1-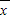 )2+(x2-
)2+(x2-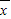 )2+…+(xn-
)2+…+(xn- )2]=a,
)2]=a, [(x1-4-
[(x1-4- -4)2+(x2-4-
-4)2+(x2-4-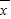 -4)2+…+(xn-4-
-4)2+…+(xn-4- -4)2]
-4)2]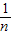 [(x1-
[(x1-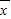 )2+(x2-
)2+(x2-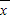 )2+…+(xn-
)2+…+(xn-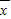 )2]=a,
)2]=a,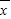 ,新數據的每一個數都乘以了3,則平均數變為3
,新數據的每一個數都乘以了3,則平均數變為3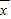 ,
,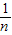 [(x1-
[(x1- )2+(x2-
)2+(x2-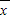 )2+…+(xn-
)2+…+(xn-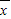 )2]=a,
)2]=a,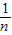 [(3x1-3
[(3x1-3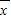 )2+(3x2-3
)2+(3x2-3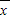 )2+…+(3xn-3
)2+…+(3xn-3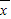 )2]
)2]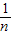 [(x1-
[(x1-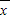 )2+(x2-
)2+(x2-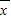 )2+…+(xn-
)2+…+(xn-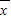 )2]
)2]

 輕松暑假總復習系列答案
輕松暑假總復習系列答案