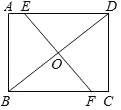
【題目】如圖，在矩形ABCD中，EF經過對角線BD的中點O，分別交AD，BC于點E，F
（1）求證：△BOF≌△DOE；
（2）若AB＝4cm，AD＝5cm，當EF⊥BD時，求四邊形ABFE的面積．
科目：初中數學 來源： 題型：
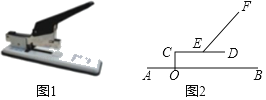
【題目】訂書機是由推動器、托板、壓形器、底座、定位軸等組成．如圖1是一臺放置在水平桌面上的大型訂書機，將其側面抽象成如圖2所示的幾何圖形．若壓形器EF的端點E固定于定位軸CD的中點處，在使用過程中，點D和點F隨壓形器及定位軸繞點C旋轉，CO⊥AB于點O，CD＝12cm連接CF，若∠FED＝45°，∠FCD＝30°．
（1）求FC的長；
（2）若OC＝2cm求在使用過程中，當點D落在底座AB上時，請計算CD與AB的夾角及點F運動的路線之長．（結果精確到0.1cm，參考數據：sin9.6°≈0.17．π≈3.14，
1.732）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在
中，
，點D為AC延長線上一點，連接BD，過A作
，垂足為M，交BC于點N
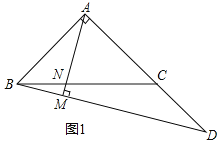
如圖1，若
，
，求AM的長；
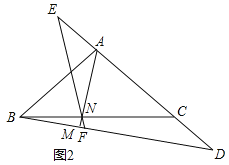
如圖2，點E在CA的延長線上，且
，連接EN并延長交BD于點F，求證：
；
在的條件下，當
時，請求出
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
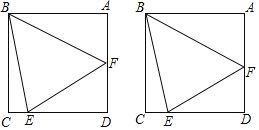
【題目】如圖，邊長為1的正方形ABCD中，點E、F分別在邊CD、AD上，連接BE、BF、EF，且有AF+CE＝EF．
（1）求(AF+1)(CE+1)的值；
（2）探究∠EBF的度數是否為定值，并說明理由；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】龍蝦狂歡季再度開啟，第
屆中國合肥龍蝦節的主題是“讓你知蝦，也知稻”，稻田小龍蝦養殖技術在合肥周邊的鄉鎮大力推廣，已知每千克小龍蝦養殖成本為
元，在整個銷售旺季的
天里，銷售單價
元/千克，與時間
（天）之間的函數關系式為：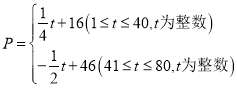
，日銷售量
（千克）與時間第（天）之間的函數關系如圖所示：
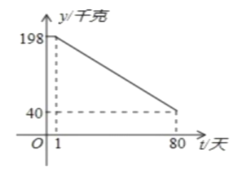
（1）求日銷售量與時間的函數關系式？
（2）哪一天的日銷售利潤最大？最大利潤是多少？
（3）在實際銷售的前
天中，該養殖戶決定銷售
千克小龍蝦，就捐贈
元給村里的特困戶，在這前天中，每天扣除捐贈后的日銷售利潤隨時間的增大而增大，求
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：若
中，其中一個內角是另一個內角的一半，則稱為“半角三角形”．
（1）若
為半角三角形，
，則其余兩個角的度數為 ．
（2）如圖1，在平行四邊形
中，
，點
在邊
上，以
為折痕，將
向上翻折，點
恰好落在
邊上的點
，若
，求證：
為半角三角形；
（3）如圖2，以的邊
為直徑畫圓，與邊
交于
，與邊
交于
，已知的面積是
面積的
倍．
①求證：
．
②若是半角三角形，
，直接寫出
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，如圖拋物線y=ax2+3ax+c（a＞0）與y軸交于點C，與x軸交于A，B兩點，點A在點B左側．點B的坐標為（1，0），OC=3OB,
（1）求拋物線的解析式；
（2）若點D是線段AC下方拋物線上的動點，求四邊形ABCD面積的最大值；
（3）若點E在x軸上，點P在拋物線上．是否存在以A，C，E，P為頂點且以AC為一邊的平行四邊形？若存在，寫出點P的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】圖①為汽車沿直線運動的速度v(m/s)與時間t(s)(0≤t≤40)之間的函數圖象．根據對此圖象的分析、理解，在圖②中畫出描述在這段時間內汽車離開出發點的路程s(m)與時間t(s)之間的函數圖象．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知拋物線
．
求出拋物線的對稱軸方程以及與
軸的交點坐標
當
時，求出拋物線與
軸的交點坐標
已知
三點構成三角形
，當拋物線與三角形的三條邊一共有
個交點時，直接寫出
的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
