【題目】某校舉行“做文明郴州人”演講比賽，聘請了10位評委為參賽選手打分，賽前，組委會擬定了四種記分方案：方案一：取所有評委所給的平均分；
方案二：在所有評委給的分中，去掉一個最高分，去掉一個最低分，取剩余得分的平均分；
方案三：取所有評委給分的中位數；
方案四：取所有評委給分的眾數．
為了探究四種記分方案的合理性，先讓一名表演選手（不參加正式比賽的）演講，讓10位評委給演講者評分，表演者得分如下表：
評委編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
打分 | 7.0 | 7.8 | 3.2 | 8.0 | 8.4 | 8.4 | 9.8 | 8.0 | 8.4 | 8.0 |
（1）請分別用上述四種方案計算表演者的得分；
（2）如果你是評委會成員，你會建議采用哪種可行的記分方案？你覺得哪幾種方案不合適？
【答案】【解答】解：（1）方案一最后得分：
（7.0+7.8+3.2+3×8+3×8.4+9.8）=7.7；
方案二最后得分：
（7.0+7.8+3×8+3×8.4）=8；
方案三最后得分：8；
方案四最后得分：8和8.4．
（2）因為方案1中的平均數受極端數值的影響，不適合作為這個同學演講的最后得分，
所以方案1不適合作為最后得分的方案；
【解析】（1）根據給出的方案和平均數的計算公式分別進行解答即可；
（2）考慮不受極值的影響，不能有兩個得分等原因進行排除，即可得出答案．
【考點精析】本題主要考查了算術平均數和中位數、眾數的相關知識點，需要掌握總數量÷總份數=平均數．解題關鍵是根據已知條件確定總數量以及與它相對應的總份數；中位數是唯一的，僅與數據的排列位置有關，它不能充分利用所有數據；眾數可能一個，也可能多個，它一定是這組數據中的數才能正確解答此題．
科目：初中數學 來源： 題型：
【題目】如圖，已知二次函數
過（﹣2，4），（﹣4，4）兩點．
（1）求二次函數
的解析式；
（2）將沿x軸翻折，再向右平移2個單位，得到拋物線
，直線y=m（m＞0）交于M、N兩點，求線段MN的長度（用含m的代數式表示）；
（3）在（2）的條件下，、交于A、B兩點，如果直線y=m與、的圖象形成的封閉曲線交于C、D兩點（C在左側），直線y=﹣m與、的圖象形成的封閉曲線交于E、F兩點（E在左側），求證：四邊形CEFD是平行四邊形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，O為原點，點A（﹣2，0），點B（0，2），點E，點F分別為OA，OB的中點．若正方形OEDF繞點O順時針旋轉，得正方形OE′D′F′，記旋轉角為α．
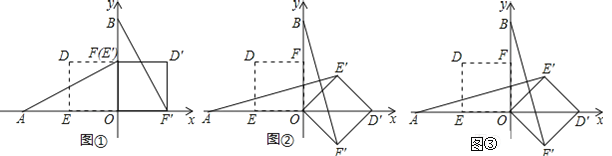
（1）如圖②，當α=135°時，求AE′，BF′的長；
（2）如圖③，當0°﹤α﹤180°時， AE′和BF′有什么位置關系；
（3）若直線AE′與直線BF′相交于點P，求點P的縱坐標的最大值（直接寫出結果即可）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知關于x的方程（x-3）(x-2)-p2=0.
（1）求證：無論p取何值時，方程總有兩個不相等的實數根；
（2）設方程兩實數根分別為x1、x2，且滿足x12+x22=3 x1x2，求實數p的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
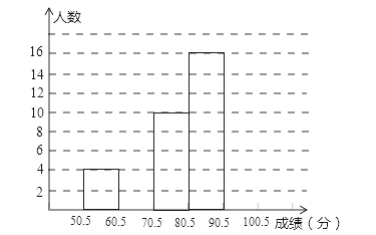
【題目】為了讓學生了解環保知識，增強環保意識，某中學舉行了一次“環保知識競賽”，共有850名學生參加了這次競賽，為了解本次競賽成績情況，從中抽取了部分學生的成績（得分取整數，滿分為100分）進行統計．請你根據尚未完成并有局部污染的頻率分布表和頻率分布直方圖，解答下列問題：
分 組 | 頻數 | 頻率 |
50.5～60.5 | 4 | 0.08 |
60.5～70.5 | 0.16 | |
70.5～80.5 | 10 | |
80.5～90.5 | 16 | 0.32 |
90.5～100.5 | ||
合 計 | 50 | 1.00 |
（1）填充頻率分布表的空格；
（2）補全頻數直方圖，并在此圖上直接繪制頻數分布折線圖；
（3）全體參賽學生中，競賽成績落在哪組范圍內的人數最多？
（4）若成績在90分以上（不含90分）為優秀，則該校成績優秀的約為多少人？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
