
【題目】如圖1,點![]() 是
是![]() 的內部一點,連接
的內部一點,連接![]() 、
、![]() 和
和![]() ,如果
,如果![]() 、
、![]() 和
和![]() 中有兩個角相等,則稱
中有兩個角相等,則稱![]() 是
是![]() 的“等心”.特別地,若這三個角都相等,則稱
的“等心”.特別地,若這三個角都相等,則稱![]() 是
是![]() 的“恒等心”.
的“恒等心”.
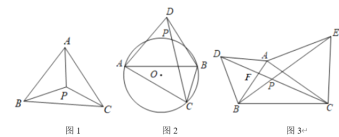
(1)在等邊![]() 中,點
中,點![]() 是恒等心,
是恒等心,![]() ,則點
,則點![]() 到
到![]() 的距離是_______;
的距離是_______;
(2)如圖2,在![]() 中,
中,![]() ,點
,點![]() 是
是![]() 的外接圓外一點,連接
的外接圓外一點,連接![]() ,交
,交![]() 于點
于點![]() ,試判斷
,試判斷![]() 是不是
是不是![]() 的“等心”,并說明理由;
的“等心”,并說明理由;
(3)如圖3,分別以銳角![]() 的邊
的邊![]() 、
、![]() 為邊向外做等邊
為邊向外做等邊![]() 和等邊
和等邊![]() ,
,![]() 和
和![]() 相交于點
相交于點![]() ,求證:點
,求證:點![]() 是
是![]() 的“恒等心”.
的“恒等心”.
【答案】(1)![]() ;(2)
;(2)![]() 是
是![]() 的“等心”,理由見解析;(3)證明見解析.
的“等心”,理由見解析;(3)證明見解析.
【解析】
(1)先根據“恒等心”的定義求出![]() ,再根據三角形全等的判定定理與性質得出
,再根據三角形全等的判定定理與性質得出![]() ,然后根據等腰三角形的性質可得
,然后根據等腰三角形的性質可得![]() ,最后解直角三角形即可得;
,最后解直角三角形即可得;
(2)先根據等腰三角形的性質可得![]() ,再根據圓周角定理可得
,再根據圓周角定理可得![]() ,從而可得
,從而可得![]() ,然后根據領補角的定義、等量代換可得
,然后根據領補角的定義、等量代換可得![]() ,最后根據圓內接四邊形的性質可得
,最后根據圓內接四邊形的性質可得![]() ,從而可得
,從而可得![]() ,由此即可得證;
,由此即可得證;
(3)如圖(見解析),先根據三角形全等的判定定理可得![]() ,從而根據三角形全等的性質可得
,從而根據三角形全等的性質可得![]() ,再根據三角形的外角性質可得
,再根據三角形的外角性質可得![]() ,從而可得
,從而可得![]() ,然后根據相似三角形的判定與性質可得
,然后根據相似三角形的判定與性質可得![]() ,又根據相似三角形的判定與性質可得
,又根據相似三角形的判定與性質可得![]() ,最后根據角的和差可得出
,最后根據角的和差可得出![]() ,由此即可得證.
,由此即可得證.
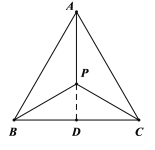
(1)如圖,過點P作![]() 于點D
于點D
由“恒等心”的定義得:![]()
![]()
![]()
![]()
![]()
![]() 是等邊三角形
是等邊三角形
![]()
![]()
在![]() 和
和![]() 中,
中,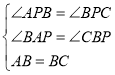
![]()
![]()
![]()
![]() (等腰三角形的三線合一)
(等腰三角形的三線合一)
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
即點![]() 到
到![]() 的距離是2
的距離是2
故答案為:![]() ;
;
(2)如圖,連接PA、PB
![]()
![]()
由圓周角定理得:![]()
![]()
又![]()
![]()
由圓內接四邊形的性質可知,![]()
![]()
![]()
![]() 是
是![]() 的“等心”;
的“等心”;

(3)如圖,連接![]()
![]() 和
和![]() 都是等邊三角形
都是等邊三角形
![]() ,
,![]() ,
,![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,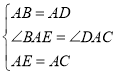
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,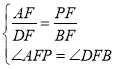
![]()
![]()
![]()
![]()
![]()
則點![]() 是
是![]() 的“恒等心”.
的“恒等心”.



科目:初中數學 來源: 題型:
【題目】某海域有A、B、C三艘船正在捕魚作業,C船突然出現故障,向A、B兩船發出緊急求救信號,此時B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏東33°方向,同時又位于B船的北偏東78°方向.
(1)求∠ABC的度數;
(2)A船以每小時30海里的速度前去救援,問多長時間能到出事地點.(結果精確到0.01小時).
(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新型冠狀病毒肺炎疫情發生后,全社會的積極參與疫情防控工作下,才有了我們的平安復學.為了能在復學前將一批防疫物資送達校園,某運輸公司組織了甲、乙兩種貨車,已知甲種貨車比乙種貨車每輛車多裝20箱防疫物資,且甲種貨車裝運900箱防疫物資所用車輛與乙種貨車裝運600箱防疫物資所用的車輛相等,求甲、乙兩種貨車每輛車可裝多少箱防疫物資?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據規定,我市將垃圾分為了四類:可回收垃圾、餐廚垃圾、有害垃圾和其他垃圾.現有投放這四類垃圾的垃圾桶各1個,若將用不透明垃圾袋分類打包好的兩袋不同垃圾隨機投人進兩個不同的垃圾桶,投放正確的概率是________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:對于平面直角坐標系![]() 中的線段
中的線段![]() 和點
和點![]() ,在
,在![]() 中,當
中,當![]() 邊上的高為2時,稱
邊上的高為2時,稱![]() 為
為![]() 的“等高點”,稱此時
的“等高點”,稱此時![]() 為
為![]() 的“等高距離”.
的“等高距離”.
(1)若點![]() 的坐標為(1,2),點
的坐標為(1,2),點![]() 的坐標為(4,2),則在點
的坐標為(4,2),則在點![]() (1,0),
(1,0),![]() (
(![]() ,4),
,4),![]() (0,3)中,
(0,3)中,![]() 的“等高點”是點___;
的“等高點”是點___;
(2)若![]() (0,0),
(0,0),![]() =2,當
=2,當![]() 的“等高點”在
的“等高點”在![]() 軸正半軸上且“等高距離”最小時,點
軸正半軸上且“等高距離”最小時,點![]() 的坐標是__.
的坐標是__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() .直線
.直線![]() 經過點
經過點![]() ,
,![]() .
.
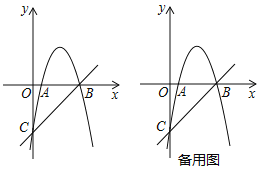
(1)求拋物線的解析式;
(2)過點![]() 的直線交直線
的直線交直線![]() 于點
于點![]() .
.
①當![]() 時,過拋物線上一動點
時,過拋物線上一動點![]() (不與點
(不與點![]() ,
,![]() 重合),作直線
重合),作直線![]() 的平行線交直線
的平行線交直線![]() 于點
于點![]() ,若以點
,若以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形,求點
為頂點的四邊形是平行四邊形,求點![]() 的橫坐標;
的橫坐標;
②連接![]() ,當直線
,當直線![]() 與直線
與直線![]() 的夾角等于
的夾角等于![]() 的
的![]() 倍時,請直接寫出點
倍時,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織學生開展義務植樹活動,在活動結束后隨機調查了40名學生每人植樹的棵數,根據調查獲取的樣本數據,制作了條形統計圖和扇形統計圖.請根據相關信息,解答下列問題:
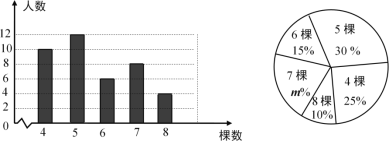
(1)扇形圖中![]() 的值是_________;
的值是_________;
(2)求隨機調查的40名學生每人植樹棵數這組數據的平均數、眾數和中位數;
(3)若本次活動九年級共有300名學生參加,估計植樹超過6棵(不含6棵)的學生約有多少人.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com